Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 166372 by mathlove last updated on 19/Feb/22

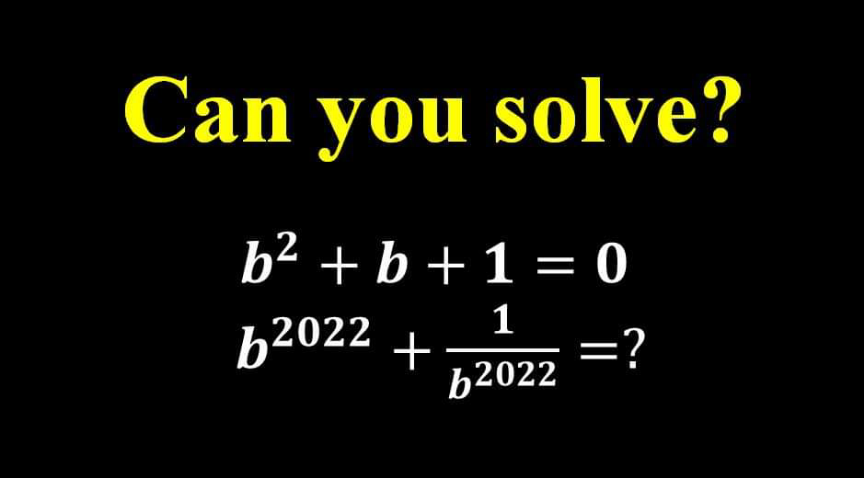
Answered by MJS_new last updated on 19/Feb/22

Yes I can.

$$\mathrm{Yes}\:\mathrm{I}\:\mathrm{can}. \\ $$

Commented by mr W last updated on 19/Feb/22

yes, we can!

$${yes},\:{we}\:{can}! \\ $$

Commented by peter frank last updated on 19/Feb/22

hahahhahah

$$\mathrm{hahahhahah} \\ $$

Answered by MathsFan last updated on 19/Feb/22

yes i can!

$$\boldsymbol{\mathrm{yes}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{can}}! \\ $$

Answered by Rasheed.Sindhi last updated on 19/Feb/22

b^2 +b+1=0⇒(b−1)(b^2 +b+1)=0 ⇒b^3 −1=0⇒b=1,ω,ω^2 ∵b=1 is the root of b−1=0 ∴b^2 +b+1⇒b=ω,ω^2 b=ω: b^(2022) +(1/b^(2022) )=ω^(2022) +(1/ω^(2022) ) =(ω^3 )^(674) +(1/((ω^3 )^(674) ))=1^(674) +(1/1^(674) )=2 b=ω^2 : b^(2022) +(1/b^(2022) )=(ω^2 )^(2022) +(1/((ω^2 )^(2022) )) =(ω^3 )^(2×674) +(1/((ω^3 )^(2×674) ))=1^(2×674) +(1/1^(2×674) )=2 Hence in both cases: b^(2022) +(1/b^(2022) )=2

$${b}^{\mathrm{2}} +{b}+\mathrm{1}=\mathrm{0}\Rightarrow\left({b}−\mathrm{1}\right)\left({b}^{\mathrm{2}} +{b}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{b}^{\mathrm{3}} −\mathrm{1}=\mathrm{0}\Rightarrow{b}=\mathrm{1},\omega,\omega^{\mathrm{2}} \\ $$$$\because{b}=\mathrm{1}\:{is}\:{the}\:{root}\:{of}\:{b}−\mathrm{1}=\mathrm{0} \\ $$$$\therefore{b}^{\mathrm{2}} +{b}+\mathrm{1}\Rightarrow{b}=\omega,\omega^{\mathrm{2}} \\ $$$${b}=\omega:\:{b}^{\mathrm{2022}} +\frac{\mathrm{1}}{{b}^{\mathrm{2022}} }=\omega^{\mathrm{2022}} +\frac{\mathrm{1}}{\omega^{\mathrm{2022}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\omega^{\mathrm{3}} \right)^{\mathrm{674}} +\frac{\mathrm{1}}{\left(\omega^{\mathrm{3}} \right)^{\mathrm{674}} }=\mathrm{1}^{\mathrm{674}} +\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{674}} }=\mathrm{2} \\ $$$${b}=\omega^{\mathrm{2}} :\:\:{b}^{\mathrm{2022}} +\frac{\mathrm{1}}{{b}^{\mathrm{2022}} }=\left(\omega^{\mathrm{2}} \right)^{\mathrm{2022}} +\frac{\mathrm{1}}{\left(\omega^{\mathrm{2}} \right)^{\mathrm{2022}} } \\ $$$$=\left(\omega^{\mathrm{3}} \right)^{\mathrm{2}×\mathrm{674}} +\frac{\mathrm{1}}{\left(\omega^{\mathrm{3}} \right)^{\mathrm{2}×\mathrm{674}} }=\mathrm{1}^{\mathrm{2}×\mathrm{674}} +\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}×\mathrm{674}} }=\mathrm{2} \\ $$$${Hence}\:{in}\:{both}\:{cases}: \\ $$$$\:{b}^{\mathrm{2022}} +\frac{\mathrm{1}}{{b}^{\mathrm{2022}} }=\mathrm{2} \\ $$

Commented by mathlove last updated on 19/Feb/22

thanks sir

$${thanks}\:{sir} \\ $$

Commented by peter frank last updated on 19/Feb/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Commented by Rasheed.Sindhi last updated on 19/Feb/22

you′re welcome!

$${you}'{re}\:{welcome}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com