
Question Number 166143 by Tawa11 last updated on 13/Feb/22
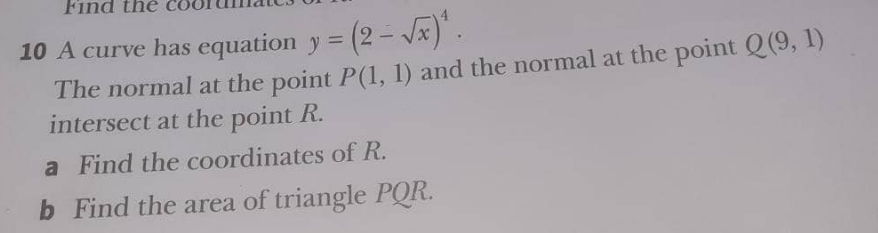
Answered by som(math1967) last updated on 14/Feb/22
![y=(2−(√x))^4 (dy/dx)=−4(2−(√x))^3 ×(1/(2(√x)))=−((2(2−(√x))^3 )/( (√x))) [(dy/dx)]_((1,1)) =((2(2−1)^3 )/1)=−2 slope of normal through P =(1/2) [(dy/dx)]_((9,1)) =−((2(2−3)^3 )/3)=(2/3) slope of normal throughQ=−(3/2) equn. of normal throughP y−1=(1/2)(x−1) ⇒x−2y=−1 equn. of normal through Q y−1=−(3/2)(x−9) ⇒3x+2y=29 by solving x=7, y=4 R(7,4) Area of △PQR=(1/2)∣1(1−4)+9(4−1) +7(1−1)∣ =(1/2)×24=12sq unit](Q166151.png)
$$\:{y}=\left(\mathrm{2}−\sqrt{{x}}\right)^{\mathrm{4}} \\ $$$$\:\frac{{dy}}{{dx}}=−\mathrm{4}\left(\mathrm{2}−\sqrt{{x}}\right)^{\mathrm{3}} ×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}=−\frac{\mathrm{2}\left(\mathrm{2}−\sqrt{{x}}\right)^{\mathrm{3}} }{\:\sqrt{{x}}} \\ $$$$\left[\frac{{dy}}{{dx}}\right]_{\left(\mathrm{1},\mathrm{1}\right)} =\frac{\mathrm{2}\left(\mathrm{2}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{1}}=−\mathrm{2} \\ $$$${slope}\:{of}\:{normal}\:{through}\:{P} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left[\frac{{dy}}{{dx}}\right]_{\left(\mathrm{9},\mathrm{1}\right)} =−\frac{\mathrm{2}\left(\mathrm{2}−\mathrm{3}\right)^{\mathrm{3}} }{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${slope}\:{of}\:{normal}\:{throughQ}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${equn}.\:{of}\:{normal}\:{throughP} \\ $$$$\:{y}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\mathrm{1}\right) \\ $$$$\Rightarrow{x}−\mathrm{2}{y}=−\mathrm{1} \\ $$$${equn}.\:{of}\:{normal}\:{through}\:{Q} \\ $$$${y}−\mathrm{1}=−\frac{\mathrm{3}}{\mathrm{2}}\left({x}−\mathrm{9}\right) \\ $$$$\Rightarrow\mathrm{3}{x}+\mathrm{2}{y}=\mathrm{29} \\ $$$${by}\:{solving}\:{x}=\mathrm{7},\:{y}=\mathrm{4} \\ $$$${R}\left(\mathrm{7},\mathrm{4}\right) \\ $$$${Area}\:{of}\:\bigtriangleup{PQR}=\frac{\mathrm{1}}{\mathrm{2}}\mid\mathrm{1}\left(\mathrm{1}−\mathrm{4}\right)+\mathrm{9}\left(\mathrm{4}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{7}\left(\mathrm{1}−\mathrm{1}\right)\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{24}=\mathrm{12}{sq}\:{unit} \\ $$$$ \\ $$$$\: \\ $$
Commented by Tawa11 last updated on 14/Feb/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by som(math1967) last updated on 14/Feb/22
$${thanks}\:{for}\:{correction} \\ $$
Commented by cortano1 last updated on 14/Feb/22
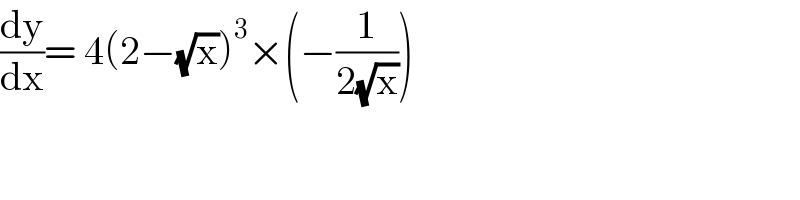
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\:\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{x}}\right)^{\mathrm{3}} ×\left(−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\right) \\ $$
