
Question Number 16613 by ajfour last updated on 24/Jun/17

Commented by ajfour last updated on 24/Jun/17

$$\mathrm{From}\:\mathrm{the}\:\mathrm{endpoint}\:\mathrm{of}\:\mathrm{a}\:\mathrm{diameter} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{sphere}\:\mathrm{draw}\:\mathrm{a}\:\mathrm{chord}\:\mathrm{so}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{surface}\:\mathrm{generated}\:\mathrm{by}\:\mathrm{a}\:\mathrm{rotation} \\ $$$$\mathrm{about}\:\mathrm{this}\:\mathrm{diameter}\:\mathrm{divides}\:\mathrm{the} \\ $$$$\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sphere}\:\mathrm{into}\:\mathrm{two} \\ $$$$\mathrm{equal}\:\mathrm{parts}.\:\mathrm{Determine}\:\mathrm{the}\:\mathrm{angle} \\ $$$$\mathrm{between}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{and}\:\mathrm{the}\:\mathrm{diameter}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 24/Jun/17

$${mr}\:{Ajfour}!\:{way}\:{your}\:{sphere}\:{is}\:{so}\:{unhappy}? \\ $$
Answered by mrW1 last updated on 26/Jun/17
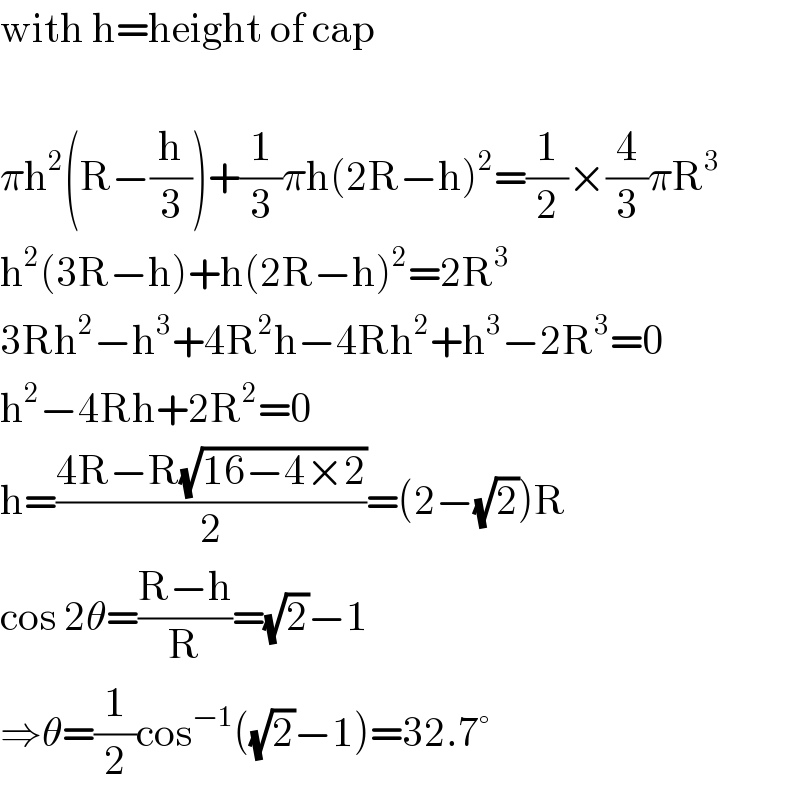
$$\mathrm{with}\:\mathrm{h}=\mathrm{height}\:\mathrm{of}\:\mathrm{cap} \\ $$$$ \\ $$$$\pi\mathrm{h}^{\mathrm{2}} \left(\mathrm{R}−\frac{\mathrm{h}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\pi\mathrm{h}\left(\mathrm{2R}−\mathrm{h}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}\pi\mathrm{R}^{\mathrm{3}} \\ $$$$\mathrm{h}^{\mathrm{2}} \left(\mathrm{3R}−\mathrm{h}\right)+\mathrm{h}\left(\mathrm{2R}−\mathrm{h}\right)^{\mathrm{2}} =\mathrm{2R}^{\mathrm{3}} \\ $$$$\mathrm{3Rh}^{\mathrm{2}} −\mathrm{h}^{\mathrm{3}} +\mathrm{4R}^{\mathrm{2}} \mathrm{h}−\mathrm{4Rh}^{\mathrm{2}} +\mathrm{h}^{\mathrm{3}} −\mathrm{2R}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{h}^{\mathrm{2}} −\mathrm{4Rh}+\mathrm{2R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{h}=\frac{\mathrm{4R}−\mathrm{R}\sqrt{\mathrm{16}−\mathrm{4}×\mathrm{2}}}{\mathrm{2}}=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\mathrm{R} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{R}−\mathrm{h}}{\mathrm{R}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\Rightarrow\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)=\mathrm{32}.\mathrm{7}° \\ $$
Commented by ajfour last updated on 26/Jun/17
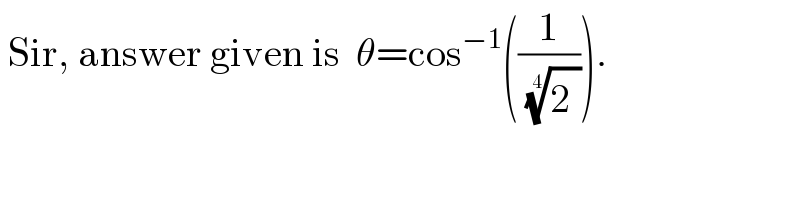
$$\:\mathrm{Sir},\:\mathrm{answer}\:\mathrm{given}\:\mathrm{is}\:\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt[{\mathrm{4}}]{\mathrm{2}^{} }}\right). \\ $$
Commented by mrW1 last updated on 26/Jun/17
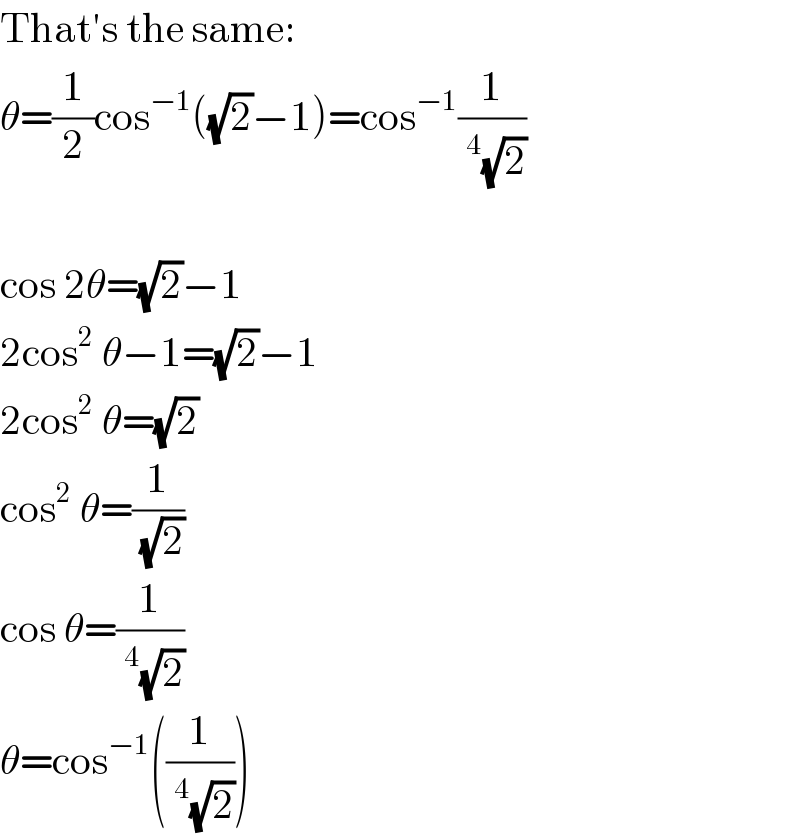
$$\mathrm{That}'\mathrm{s}\:\mathrm{the}\:\mathrm{same}: \\ $$$$\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{2}}} \\ $$$$ \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \:\theta−\mathrm{1}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \:\theta=\sqrt{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\theta=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{2}}} \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{2}}}\right) \\ $$
