Question Number 166007 by mr W last updated on 11/Feb/22
Commented by mr W last updated on 12/Feb/22
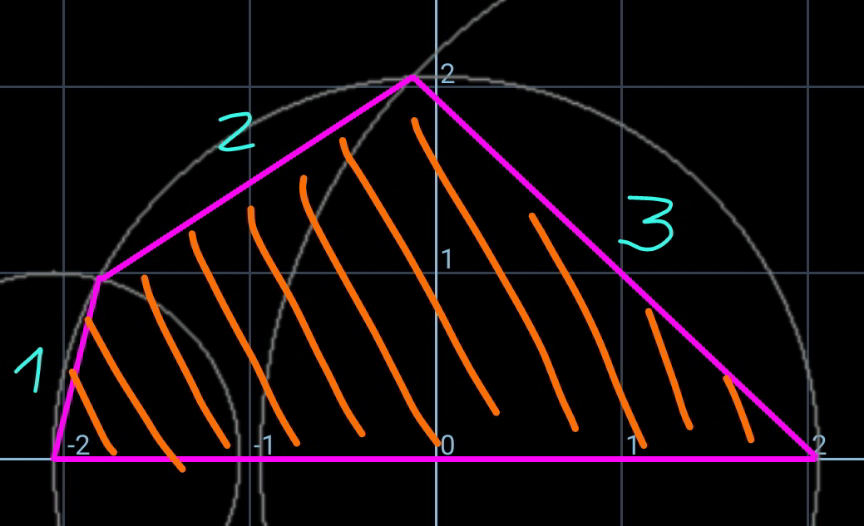
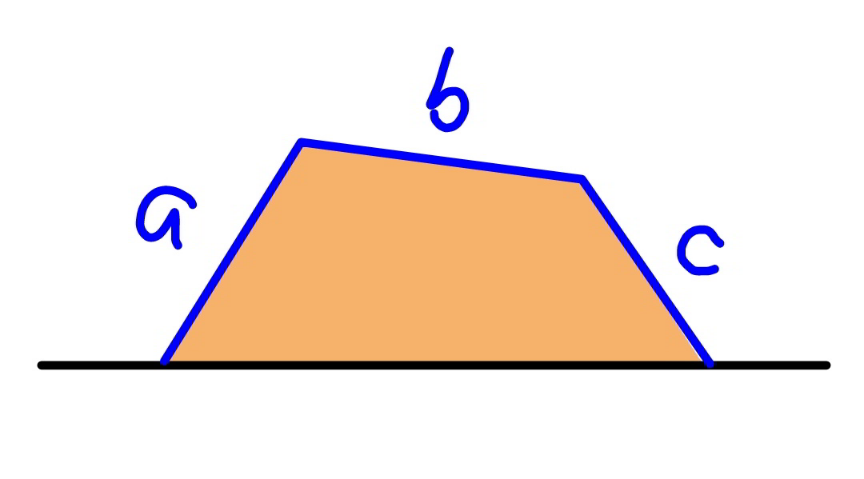
![find the maximum coloured area in terms of a, b, c. [related to Q165965 from ajfour sir]](Q166008.png)
$${find}\:{the}\:{maximum}\:{coloured}\:{area} \\ $$$${in}\:{terms}\:{of}\:{a},\:{b},\:{c}. \\ $$$$ \\ $$$$\left[{related}\:{to}\:{Q}\mathrm{165965}\:{from}\:{ajfour}\:{sir}\right] \\ $$
Answered by mr W last updated on 12/Feb/22
Commented by mr W last updated on 12/Feb/22
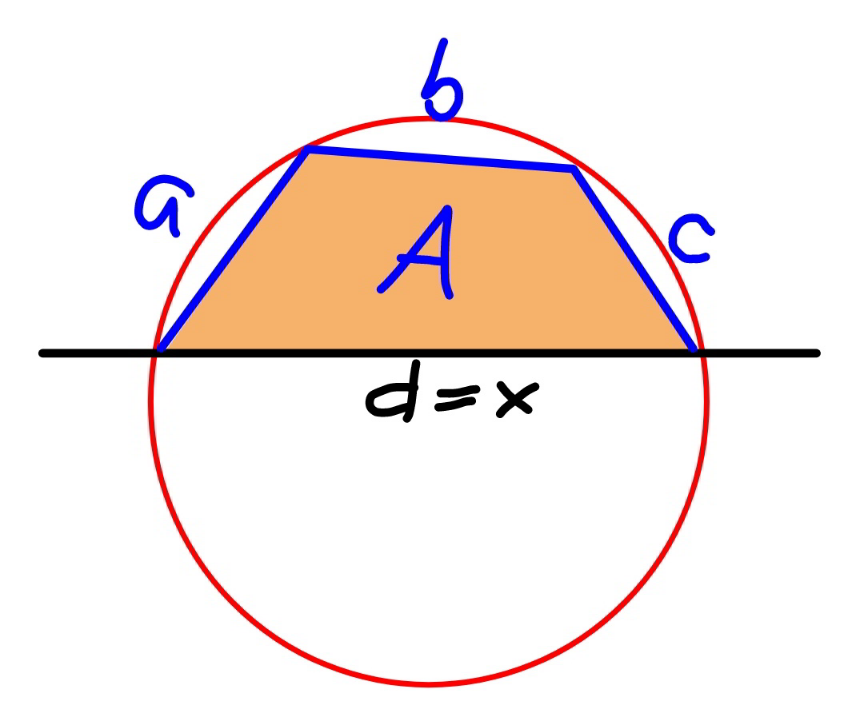
![say the fourth side on the wall has the length d=variable x. from the bretschneider′s formula for the area of a general quadrilateral with sides a, b, c, d we can see that the area of the quadrilateral is maximum, when the quadrilateral is cyclic, as the diagram above shows. the area is A=(√((s−a)(s−b)(s−c)(s−d))) with s=((a+b+c+d)/2) let Φ=A^2 Φ=(s−a)(s−b)(s−c)(s−d) ln Φ=ln (s−a)+ln (s−b)+ln (s−c)+ln (s−d) ((Φ′)/Φ)=(1/2)((1/(s−a))+(1/(s−b))+(1/(s−c))−(1/(s−d))) such that A is maximum, Φ′=(dΦ/dd)=0 (1/(s−a))+(1/(s−b))+(1/(s−c))−(1/(s−d))=0 (1/(s−a))+(1/(s−b))=(1/(s−d))−(1/(s−c)) ((2s−(a+b))/(s^2 −(a+b)s+ab))=((d−c)/(s^2 −(c+d)s+cd)) 2s^3 −(a+b+c+3d)s^2 +2d(a+b+c)s+abc−(ab+bc+ca)d=0 d^3 −(a^2 +b^2 +c^2 )d−2abc=0 ⇒d=2(√((a^2 +b^2 +c^2 )/3)) sin {(π/3)+(1/3)sin^(−1) [abc((3/(a^2 +b^2 +c^2 )))^(3/2) ]}](Q166039.png)
$${say}\:{the}\:{fourth}\:{side}\:{on}\:{the}\:{wall}\:{has}\:{the}\: \\ $$$${length}\:{d}={variable}\:{x}. \\ $$$${from}\:{the}\:{bretschneider}'{s}\:{formula}\:{for} \\ $$$${the}\:{area}\:{of}\:{a}\:{general}\:{quadrilateral} \\ $$$${with}\:{sides}\:{a},\:{b},\:{c},\:{d}\:{we}\:{can}\:{see}\:{that}\:{the} \\ $$$${area}\:{of}\:{the}\:{quadrilateral}\:{is}\:{maximum}, \\ $$$${when}\:{the}\:{quadrilateral}\:{is}\:{cyclic},\:{as} \\ $$$${the}\:{diagram}\:{above}\:{shows}. \\ $$$${the}\:{area}\:{is} \\ $$$${A}=\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{d}\right)} \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}+{d}}{\mathrm{2}} \\ $$$${let}\:\Phi={A}^{\mathrm{2}} \\ $$$$\Phi=\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{d}\right) \\ $$$$\mathrm{ln}\:\Phi=\mathrm{ln}\:\left({s}−{a}\right)+\mathrm{ln}\:\left({s}−{b}\right)+\mathrm{ln}\:\left({s}−{c}\right)+\mathrm{ln}\:\left({s}−{d}\right) \\ $$$$\frac{\Phi'}{\Phi}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{s}−{a}}+\frac{\mathrm{1}}{{s}−{b}}+\frac{\mathrm{1}}{{s}−{c}}−\frac{\mathrm{1}}{{s}−{d}}\right) \\ $$$${such}\:{that}\:{A}\:{is}\:{maximum},\:\Phi'=\frac{{d}\Phi}{{dd}}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{s}−{a}}+\frac{\mathrm{1}}{{s}−{b}}+\frac{\mathrm{1}}{{s}−{c}}−\frac{\mathrm{1}}{{s}−{d}}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{s}−{a}}+\frac{\mathrm{1}}{{s}−{b}}=\frac{\mathrm{1}}{{s}−{d}}−\frac{\mathrm{1}}{{s}−{c}} \\ $$$$\frac{\mathrm{2}{s}−\left({a}+{b}\right)}{{s}^{\mathrm{2}} −\left({a}+{b}\right){s}+{ab}}=\frac{{d}−{c}}{{s}^{\mathrm{2}} −\left({c}+{d}\right){s}+{cd}} \\ $$$$\mathrm{2}{s}^{\mathrm{3}} −\left({a}+{b}+{c}+\mathrm{3}{d}\right){s}^{\mathrm{2}} +\mathrm{2}{d}\left({a}+{b}+{c}\right){s}+{abc}−\left({ab}+{bc}+{ca}\right){d}=\mathrm{0} \\ $$$${d}^{\mathrm{3}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){d}−\mathrm{2}{abc}=\mathrm{0} \\ $$$$\Rightarrow{d}=\mathrm{2}\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}}\:\mathrm{sin}\:\left\{\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \left[{abc}\left(\frac{\mathrm{3}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]\right\} \\ $$
Commented by mr W last updated on 12/Feb/22

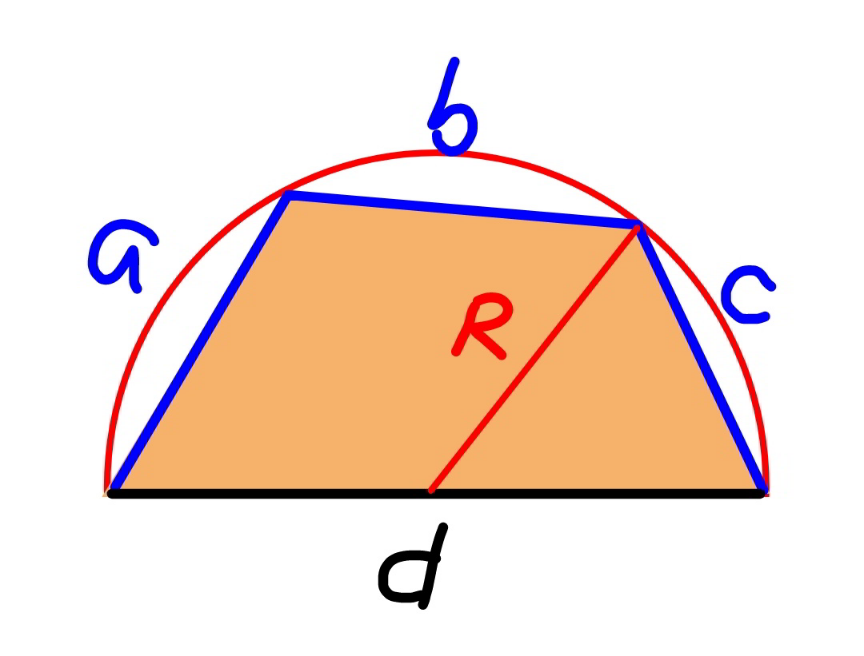
$${further}\:{study}\:{shows}\:{that}\:{in}\:{this}\:{case} \\ $$$${the}\:{corresponding}\:{maximum}\:{area}\:{is} \\ $$$${when}\:{the}\:{sides}\:{a},\:{b},\:{c}\:{are}\:{the}\:{chords}\: \\ $$$${on}\:{a}\:{semicircle}\:{with}\:{diameter}\:{d}\:{which} \\ $$$${can}\:{be}\:{calculated}\:{according}\:{to}\:{the}\: \\ $$$${formula}\:{above}. \\ $$
Commented by mr W last updated on 12/Feb/22
Commented by mr W last updated on 12/Feb/22
Bretschneider's formula: https://en.m.wikipedia.org/wiki/Bretschneider%27s_formula
Commented by mr W last updated on 12/Feb/22