Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 165969 by leicianocosta last updated on 10/Feb/22

$$ \\ $$

Commented by leicianocosta last updated on 10/Feb/22

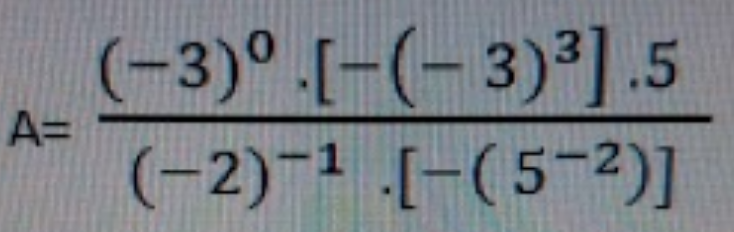
Commented by hknkrc46 last updated on 10/Feb/22

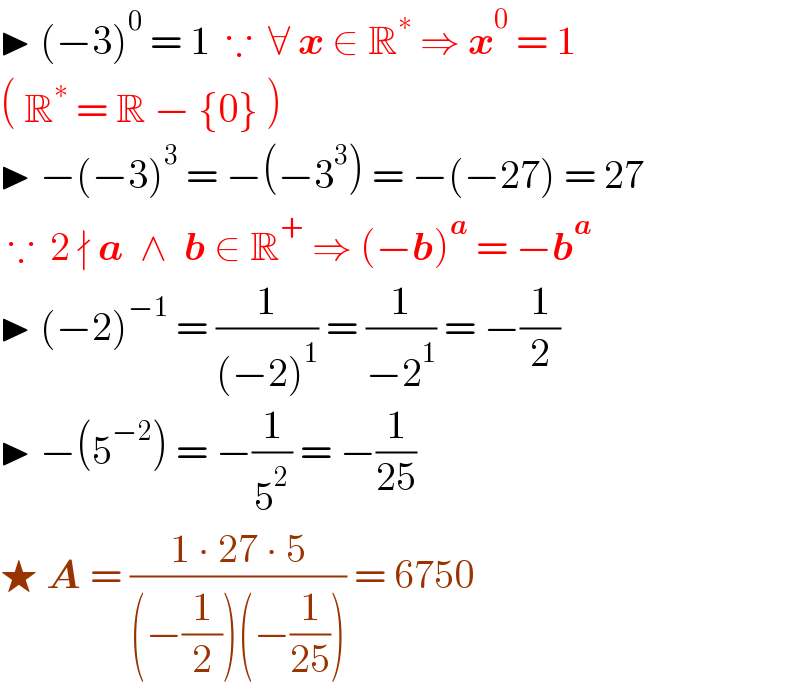
▶ (−3)^0 = 1 ∵ ∀ x ∈ R^∗ ⇒ x^0 = 1 ( R^∗ = R − {0} ) ▶ −(−3)^3 = −(−3^3 ) = −(−27) = 27 ∵ 2 ∤ a ∧ b ∈ R^+ ⇒ (−b)^a = −b^a ▶ (−2)^(−1) = (1/((−2)^1 )) = (1/(−2^1 )) = −(1/2) ▶ −(5^(−2) ) = −(1/5^2 ) = −(1/(25)) ★ A = ((1 ∙ 27 ∙ 5)/((−(1/2))(−(1/(25))))) = 6750

$$\blacktriangleright\:\left(−\mathrm{3}\right)^{\mathrm{0}} \:=\:\mathrm{1}\:\:\because\:\:\forall\:\boldsymbol{{x}}\:\in\:\mathbb{R}^{\ast} \:\Rightarrow\:\boldsymbol{{x}}^{\mathrm{0}} \:=\:\mathrm{1} \\ $$$$\left(\:\mathbb{R}^{\ast} \:=\:\mathbb{R}\:−\:\left\{\mathrm{0}\right\}\:\right) \\ $$$$\blacktriangleright\:−\left(−\mathrm{3}\right)^{\mathrm{3}} \:=\:−\left(−\mathrm{3}^{\mathrm{3}} \right)\:=\:−\left(−\mathrm{27}\right)\:=\:\mathrm{27} \\ $$$$\:\because\:\:\mathrm{2}\:\nmid\:\boldsymbol{{a}}\:\:\wedge\:\:\boldsymbol{{b}}\:\in\:\mathbb{R}^{+} \:\Rightarrow\:\left(−\boldsymbol{{b}}\right)^{\boldsymbol{{a}}} \:=\:−\boldsymbol{{b}}^{\boldsymbol{{a}}} \\ $$$$\blacktriangleright\:\left(−\mathrm{2}\right)^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\left(−\mathrm{2}\right)^{\mathrm{1}} }\:=\:\frac{\mathrm{1}}{−\mathrm{2}^{\mathrm{1}} }\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\blacktriangleright\:−\left(\mathrm{5}^{−\mathrm{2}} \right)\:=\:−\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\:=\:−\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$\bigstar\:\boldsymbol{{A}}\:=\:\frac{\mathrm{1}\:\centerdot\:\mathrm{27}\:\centerdot\:\mathrm{5}}{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{1}}{\mathrm{25}}\right)}\:=\:\mathrm{6750} \\ $$

Commented by alephzero last updated on 11/Feb/22

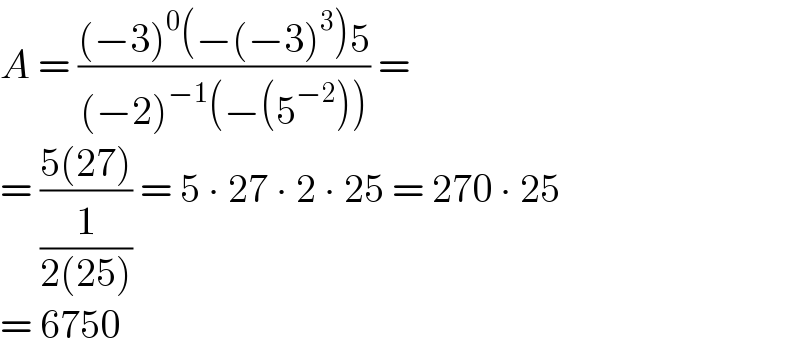
A = (((−3)^0 (−(−3)^3 )5)/((−2)^(−1) (−(5^(−2) )))) = = ((5(27))/(1/(2(25)))) = 5 ∙ 27 ∙ 2 ∙ 25 = 270 ∙ 25 = 6750

$${A}\:=\:\frac{\left(−\mathrm{3}\right)^{\mathrm{0}} \left(−\left(−\mathrm{3}\right)^{\mathrm{3}} \right)\mathrm{5}}{\left(−\mathrm{2}\right)^{−\mathrm{1}} \left(−\left(\mathrm{5}^{−\mathrm{2}} \right)\right)}\:= \\ $$$$=\:\frac{\mathrm{5}\left(\mathrm{27}\right)}{\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{25}\right)}}\:=\:\mathrm{5}\:\centerdot\:\mathrm{27}\:\centerdot\:\mathrm{2}\:\centerdot\:\mathrm{25}\:=\:\mathrm{270}\:\centerdot\:\mathrm{25} \\ $$$$=\:\mathrm{6750} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com