
Question Number 165893 by Tawa11 last updated on 09/Feb/22

Commented by otchereabdullai@gmail.com last updated on 18/Feb/22

$$\mathrm{nice} \\ $$
Answered by som(math1967) last updated on 10/Feb/22
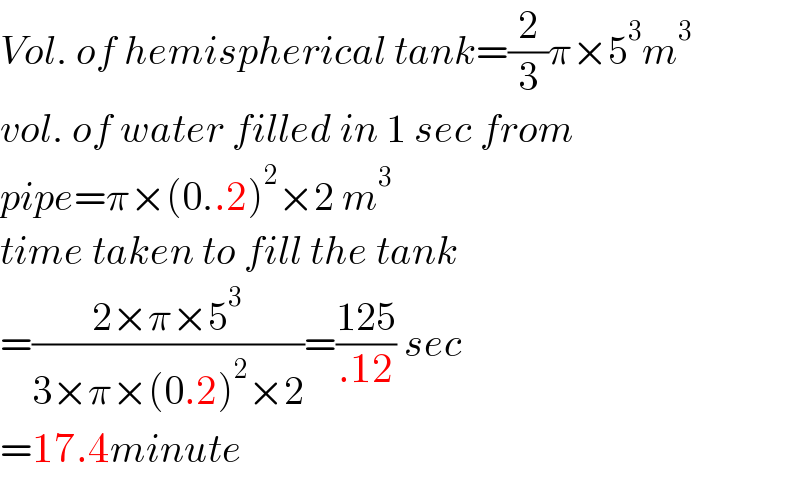
$${Vol}.\:{of}\:{hemispherical}\:{tank}=\frac{\mathrm{2}}{\mathrm{3}}\pi×\mathrm{5}^{\mathrm{3}} {m}^{\mathrm{3}} \\ $$$${vol}.\:{of}\:{water}\:{filled}\:{in}\:\mathrm{1}\:{sec}\:{from} \\ $$$${pipe}=\pi×\left(\mathrm{0}..\mathrm{2}\right)^{\mathrm{2}} ×\mathrm{2}\:{m}^{\mathrm{3}} \\ $$$${time}\:{taken}\:{to}\:{fill}\:{the}\:{tank} \\ $$$$=\frac{\mathrm{2}×\pi×\mathrm{5}^{\mathrm{3}} }{\mathrm{3}×\pi×\left(\mathrm{0}.\mathrm{2}\right)^{\mathrm{2}} ×\mathrm{2}}=\frac{\mathrm{125}}{.\mathrm{12}}\:{sec} \\ $$$$=\mathrm{17}.\mathrm{4}{minute} \\ $$
Commented by Tawa11 last updated on 10/Feb/22

$$\mathrm{Thanks}\:\mathrm{sirs}. \\ $$
Commented by Tawa11 last updated on 10/Feb/22

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 10/Feb/22

$$\mathrm{Som}\:\mathrm{sir}.\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{effort}. \\ $$
