Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 163833 by mathlove last updated on 11/Jan/22

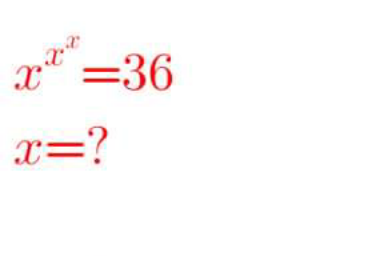
Commented by mr W last updated on 11/Jan/22

x=W^(∼) (36)≈2.107036463957

$${x}=\overset{\sim} {\boldsymbol{\mathcal{W}}}\left(\mathrm{36}\right)\approx\mathrm{2}.\mathrm{107036463957} \\ $$

Commented by Tawa11 last updated on 11/Jan/22

Sir, please show workings.

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{show}\:\mathrm{workings}. \\ $$

Commented by mr W last updated on 11/Jan/22

there is no workings! it can only be approximated. W^∼ (x) is just for fun. mr W has defined this new function as the inverse function of the function f(x)=x^x^x . i.e. W^∼ (x)^(W^∼ (x)^(W^∼ (x)) ) =x. or if y=x^x^x , then x=W^∼ (y). since mr W is a nobody, his new function W^∼ (x) is not yet popular. you are the second person in the word at all who knows about the existence of such a function. keep this for yourself! quite different is it with mr Lambert. he defined a new function W(x) as the inverse function of the function f(x)=xe^x , i.e. W(x)e^(W(x)) =x. but his function W(x) is well known. even you and i know it.

$${there}\:{is}\:{no}\:{workings}!\:{it}\:{can}\:{only}\:{be} \\ $$$${approximated}. \\ $$$$\overset{\sim} {\boldsymbol{\mathcal{W}}}\left({x}\right)\:{is}\:{just}\:{for}\:{fun}.\:{mr}\:\boldsymbol{\mathcal{W}}\:{has} \\ $$$${defined}\:{this}\:{new}\:{function}\:{as}\:{the} \\ $$$${inverse}\:{function}\:{of}\:{the}\:{function} \\ $$$${f}\left({x}\right)={x}^{{x}^{{x}} } .\:{i}.{e}.\:\overset{\sim} {\boldsymbol{\mathcal{W}}}\left({x}\right)^{\overset{\sim} {\boldsymbol{\mathcal{W}}}\left({x}\right)^{\overset{\sim} {\boldsymbol{\mathcal{W}}}\left({x}\right)} } ={x}.\:{or} \\ $$$${if}\:{y}={x}^{{x}^{{x}} } ,\:{then}\:{x}=\overset{\sim} {\boldsymbol{\mathcal{W}}}\left({y}\right).\:{since}\:{mr}\:\boldsymbol{\mathcal{W}} \\ $$$${is}\:{a}\:{nobody},\:{his}\:{new}\:{function}\:\overset{\sim} {\boldsymbol{\mathcal{W}}}\left({x}\right) \\ $$$${is}\:{not}\:{yet}\:{popular}.\:{you}\:{are}\:{the}\:{second} \\ $$$${person}\:{in}\:{the}\:{word}\:{at}\:{all}\:{who}\:{knows}\: \\ $$$${about}\:{the}\:{existence}\:{of}\:{such}\:{a}\: \\ $$$${function}.\:{keep}\:{this}\:{for}\:{yourself}! \\ $$$${quite}\:{different}\:{is}\:{it}\:{with}\:{mr}\:{Lambert}. \\ $$$${he}\:{defined}\:{a}\:{new}\:{function}\:{W}\left({x}\right)\:{as} \\ $$$${the}\:{inverse}\:{function}\:{of}\:{the}\:{function} \\ $$$${f}\left({x}\right)={xe}^{{x}} ,\:{i}.{e}.\:{W}\left({x}\right){e}^{{W}\left({x}\right)} ={x}. \\ $$$${but}\:{his}\:{function}\:{W}\left({x}\right)\:{is}\:{well}\:{known}. \\ $$$${even}\:{you}\:{and}\:{i}\:{know}\:{it}. \\ $$

Commented by Tawa11 last updated on 11/Jan/22

Wow, this is great sir. God will crown your effort sir.

$$\mathrm{Wow},\:\mathrm{this}\:\mathrm{is}\:\mathrm{great}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{will}\:\mathrm{crown}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}. \\ $$

Commented by alephzero last updated on 11/Jan/22

Great sir! But could you clarify the clear definition of the W−function?

$$\mathrm{Great}\:\mathrm{sir}!\:\mathrm{But}\:\mathrm{could}\:\mathrm{you}\:\mathrm{clarify} \\ $$$$\mathrm{the}\:\mathrm{clear}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{the}\:\mathcal{W}−\mathrm{function}? \\ $$

Commented by mr W last updated on 11/Jan/22

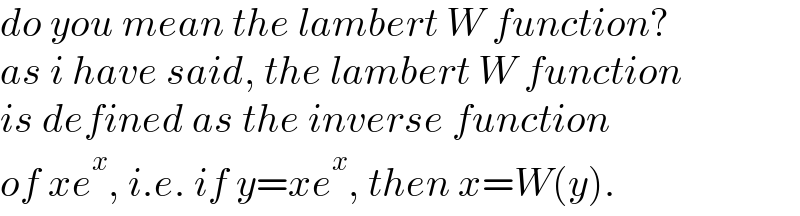
do you mean the lambert W function? as i have said, the lambert W function is defined as the inverse function of xe^x , i.e. if y=xe^x , then x=W(y).

$${do}\:{you}\:{mean}\:{the}\:{lambert}\:{W}\:{function}? \\ $$$${as}\:{i}\:{have}\:{said},\:{the}\:{lambert}\:{W}\:{function} \\ $$$${is}\:{defined}\:{as}\:{the}\:{inverse}\:{function} \\ $$$${of}\:{xe}^{{x}} ,\:{i}.{e}.\:{if}\:{y}={xe}^{{x}} ,\:{then}\:{x}={W}\left({y}\right). \\ $$

Commented by alephzero last updated on 12/Jan/22

No! I mean Your function, mr. W! W(x) = ? And what about the name?

$$\mathrm{No}!\:\mathrm{I}\:\mathrm{mean}\:\mathrm{Your}\:\mathrm{function},\:\mathrm{mr}.\:\boldsymbol{\mathcal{W}}! \\ $$$$\mathbb{W}\left({x}\right)\:=\:? \\ $$$$\mathrm{And}\:\mathrm{what}\:\mathrm{about}\:\mathrm{the}\:\mathrm{name}? \\ $$

Commented by mr W last updated on 12/Jan/22

you shouldn′t take it serious! it′s just for fun! but when you want to know, W^∼ (x) is just defined as the inverse function of f(x)=x^x^x , i.e. it fulfills W^∼ (x)^(W^∼ (x)^(W^∼ (x)) ) =x. you can not ask W^∼ (x)=?, because it′s a definition. Name of this useless function? i don′t know. what′s your suggestion?

$${you}\:{shouldn}'{t}\:{take}\:{it}\:{serious}!\:{it}'{s}\:{just} \\ $$$${for}\:{fun}!\: \\ $$$${but}\:{when}\:{you}\:{want}\:{to}\:{know}, \\ $$$$\overset{\sim} {{W}}\left({x}\right)\:{is}\:{just}\:{defined}\:{as}\:{the}\:{inverse} \\ $$$${function}\:{of}\:{f}\left({x}\right)={x}^{{x}^{{x}} } ,\:\:{i}.{e}.\:{it}\:{fulfills} \\ $$$$\overset{\sim} {{W}}\left({x}\right)^{\overset{\sim} {{W}}\left({x}\right)^{\overset{\sim} {{W}}\left({x}\right)} } ={x}.\: \\ $$$${you}\:{can}\:{not}\:{ask}\:\overset{\sim} {{W}}\left({x}\right)=?,\:\:{because}\: \\ $$$${it}'{s}\:{a}\:{definition}. \\ $$$$ \\ $$$${Name}\:{of}\:{this}\:{useless}\:{function}? \\ $$$${i}\:{don}'{t}\:{know}.\:{what}'{s}\:{your}\:{suggestion}? \\ $$

Commented by alephzero last updated on 12/Jan/22

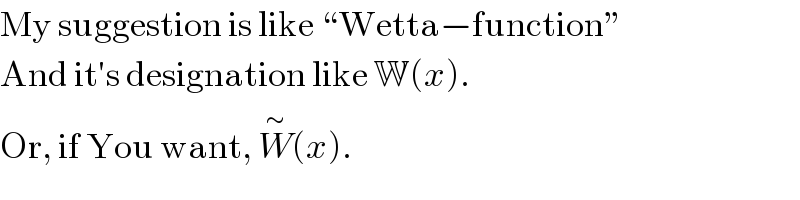
My suggestion is like “Wetta−function” And it′s designation like W(x). Or, if You want, W^∼ (x).

$$\mathrm{My}\:\mathrm{suggestion}\:\mathrm{is}\:\mathrm{like}\:``\mathrm{Wetta}−\mathrm{function}'' \\ $$$$\mathrm{And}\:\mathrm{it}'\mathrm{s}\:\mathrm{designation}\:\mathrm{like}\:\mathbb{W}\left({x}\right). \\ $$$$\mathrm{Or},\:\mathrm{if}\:\mathrm{You}\:\mathrm{want},\:\overset{\sim} {{W}}\left({x}\right). \\ $$

Commented by Tawa11 last updated on 15/Jan/22

Sir mrW. Please how did you press or get the approximation.

$$\mathrm{Sir}\:\mathrm{mrW}.\:\:\mathrm{Please}\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{press}\:\mathrm{or}\:\mathrm{get}\:\mathrm{the}\:\mathrm{approximation}. \\ $$

Commented by mr W last updated on 15/Jan/22

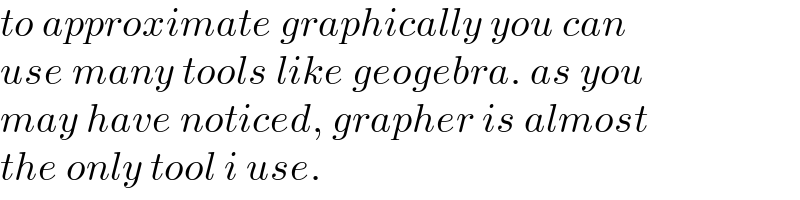
to approximate graphically you can use many tools like geogebra. as you may have noticed, grapher is almost the only tool i use.

$${to}\:{approximate}\:{graphically}\:{you}\:{can} \\ $$$${use}\:{many}\:{tools}\:{like}\:{geogebra}.\:{as}\:{you} \\ $$$${may}\:{have}\:{noticed},\:{grapher}\:{is}\:{almost} \\ $$$${the}\:{only}\:{tool}\:{i}\:{use}. \\ $$

Commented by Tawa11 last updated on 15/Jan/22

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by Gbenga last updated on 11/Jan/22

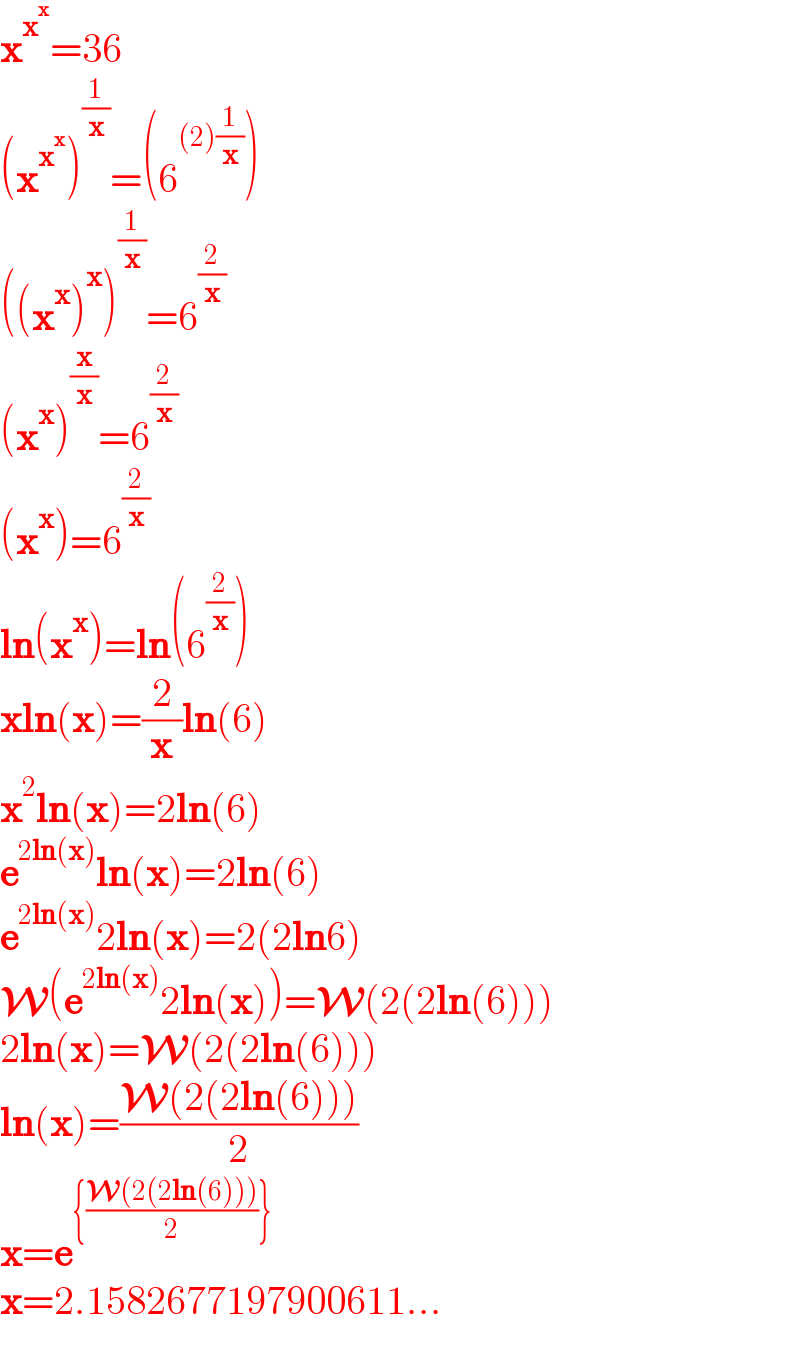
x^x^x =36 (x^x^x )^(1/x) =(6^((2)(1/x)) ) ((x^x )^x )^(1/x) =6^(2/x) (x^x )^(x/x) =6^(2/x) (x^x )=6^(2/x) ln(x^x )=ln(6^(2/x) ) xln(x)=(2/x)ln(6) x^2 ln(x)=2ln(6) e^(2ln(x)) ln(x)=2ln(6) e^(2ln(x)) 2ln(x)=2(2ln6) W(e^(2ln(x)) 2ln(x))=W(2(2ln(6))) 2ln(x)=W(2(2ln(6))) ln(x)=((W(2(2ln(6))))/2) x=e^({((W(2(2ln(6))))/2)}) x=2.1582677197900611...

$$\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} } =\mathrm{36} \\ $$$$\left(\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} } \right)^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}} =\left(\mathrm{6}^{\left(\mathrm{2}\right)\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}} \right) \\ $$$$\left(\left(\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} \right)^{\boldsymbol{\mathrm{x}}} \right)^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}} =\mathrm{6}^{\frac{\mathrm{2}}{\boldsymbol{\mathrm{x}}}} \\ $$$$\left(\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} \right)^{\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}}} =\mathrm{6}^{\frac{\mathrm{2}}{\boldsymbol{\mathrm{x}}}} \\ $$$$\left(\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} \right)=\mathrm{6}^{\frac{\mathrm{2}}{\boldsymbol{\mathrm{x}}}} \\ $$$$\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} \right)=\boldsymbol{\mathrm{ln}}\left(\mathrm{6}^{\frac{\mathrm{2}}{\boldsymbol{\mathrm{x}}}} \right) \\ $$$$\boldsymbol{\mathrm{xln}}\left(\boldsymbol{\mathrm{x}}\right)=\frac{\mathrm{2}}{\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right) \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right) \\ $$$$\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right) \\ $$$$\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)} \mathrm{2}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{2}\left(\mathrm{2}\boldsymbol{\mathrm{ln}}\mathrm{6}\right) \\ $$$$\boldsymbol{\mathcal{W}}\left(\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)} \mathrm{2}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\right)=\boldsymbol{\mathcal{W}}\left(\mathrm{2}\left(\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right)\right)\right) \\ $$$$\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)=\boldsymbol{\mathcal{W}}\left(\mathrm{2}\left(\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right)\right)\right) \\ $$$$\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)=\frac{\boldsymbol{\mathcal{W}}\left(\mathrm{2}\left(\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right)\right)\right)}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{e}}^{\left\{\frac{\boldsymbol{\mathcal{W}}\left(\mathrm{2}\left(\mathrm{2}\boldsymbol{\mathrm{ln}}\left(\mathrm{6}\right)\right)\right)}{\mathrm{2}}\right\}} \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{2}.\mathrm{1582677197900611}... \\ $$

Commented by mr W last updated on 11/Jan/22

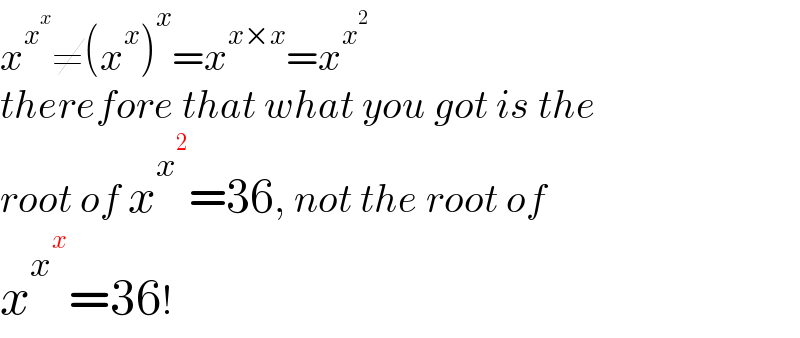
x^x^x ≠(x^x )^x =x^(x×x) =x^x^2 therefore that what you got is the root of x^x^2 =36, not the root of x^x^x =36!

$${x}^{{x}^{{x}} } \neq\left({x}^{{x}} \right)^{{x}} ={x}^{{x}×{x}} ={x}^{{x}^{\mathrm{2}} } \\ $$$${therefore}\:{that}\:{what}\:{you}\:{got}\:{is}\:{the} \\ $$$${root}\:{of}\:{x}^{{x}^{\mathrm{2}} } =\mathrm{36},\:{not}\:{the}\:{root}\:{of} \\ $$$${x}^{{x}^{{x}} } =\mathrm{36}! \\ $$

Commented by mr W last updated on 11/Jan/22

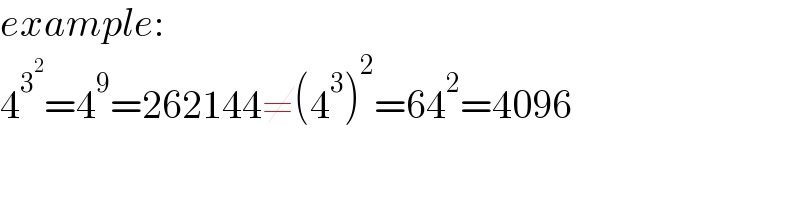
example: 4^3^2 =4^9 =262144≠(4^3 )^2 =64^2 =4096

$${example}: \\ $$$$\mathrm{4}^{\mathrm{3}^{\mathrm{2}} } =\mathrm{4}^{\mathrm{9}} =\mathrm{262144}\neq\left(\mathrm{4}^{\mathrm{3}} \right)^{\mathrm{2}} =\mathrm{64}^{\mathrm{2}} =\mathrm{4096} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com