Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 163178 by Tawa11 last updated on 04/Jan/22

Answered by mr W last updated on 05/Jan/22

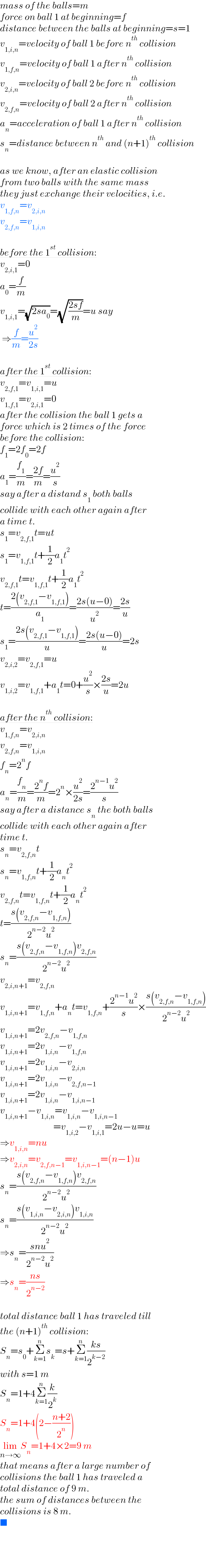
mass of the balls=m force on ball 1 at beginning=f distance between the balls at beginning=s=1 v_(1,i,n) =velocity of ball 1 before n^(th) collision v_(1,f,n) =velocity of ball 1 after n^(th) collision v_(2,i,n) =velocity of ball 2 before n^(th) collision v_(2,f,n) =velocity of ball 2 after n^(th) collision a_n =acceleration of ball 1 after n^(th) collision s_n =distance between n^(th) and (n+1)^(th) collision as we know, after an elastic collision from two balls with the same mass they just exchange their velocities, i.e. v_(1,f,n) =v_(2,i,n) v_(2,f,n) =v_(1,i,n) before the 1^(st) collision: v_(2,i,1) =0 a_0 =(f/m) v_(1,i,1) =(√(2sa_0 ))=(√((2sf)/m))=u say ⇒(f/m)=(u^2 /(2s)) after the 1^(st) collision: v_(2,f,1) =v_(1,i,1) =u v_(1,f,1) =v_(2,i,1) =0 after the collision the ball 1 gets a force which is 2 times of the force before the collision: f_1 =2f_0 =2f a_1 =(f_1 /m)=((2f)/m)=(u^2 /s) say after a distand s_1 both balls collide with each other again after a time t. s_1 =v_(2,f,1) t=ut s_1 =v_(1,f,1) t+(1/2)a_1 t^2 v_(2,f,1) t=v_(1,f,1) t+(1/2)a_1 t^2 t=((2(v_(2,f,1) −v_(1,f,1) ))/a_1 )=((2s(u−0))/u^2 )=((2s)/u) s_1 =((2s(v_(2,f,1) −v_(1,f,1) ))/u)=((2s(u−0))/u)=2s v_(2,i,2) =v_(2,f,1) =u v_(1,i,2) =v_(1,f,1) +a_1 t=0+(u^2 /s)×((2s)/u)=2u after the n^(th) collision: v_(1,f,n) =v_(2,i,n) v_(2,f,n) =v_(1,i,n) f_n =2^n f a_n =(f_n /m)=((2^n f)/m)=2^n ×(u^2 /(2s))=((2^(n−1) u^2 )/s) say after a distance s_n the both balls collide with each other again after time t. s_n =v_(2,f,n) t s_n =v_(1,f,n) t+(1/2)a_n t^2 v_(2,f,n) t=v_(1,f,n) t+(1/2)a_n t^2 t=((s(v_(2,f,n) −v_(1,f,n) ))/(2^(n−2) u^2 )) s_n =((s(v_(2,f,n) −v_(1,f,n) )v_(2,f,n) )/(2^(n−2) u^2 )) v_(2,i,n+1) =v_(2,f,n) v_(1,i,n+1) =v_(1,f,n) +a_n t=v_(1,f,n) +((2^(n−1) u^2 )/s)×((s(v_(2,f,n) −v_(1,f,n) ))/(2^(n−2) u^2 )) v_(1,i,n+1) =2v_(2,f,n) −v_(1,f,n) v_(1,i,n+1) =2v_(1,i,n) −v_(1,f,n) v_(1,i,n+1) =2v_(1,i,n) −v_(2,i,n) v_(1,i,n+1) =2v_(1,i,n) −v_(2,f,n−1) v_(1,i,n+1) =2v_(1,i,n) −v_(1,i,n−1) v_(1,i,n+1) −v_(1,i,n) =v_(1,i,n) −v_(1,i,n−1) =v_(1,i,2) −v_(1,i,1) =2u−u=u ⇒v_(1,i,n) =nu ⇒v_(2,i,n) =v_(2,f,n−1) =v_(1,i,n−1) =(n−1)u s_n =((s(v_(2,f,n) −v_(1,f,n) )v_(2,f,n) )/(2^(n−2) u^2 )) s_n =((s(v_(1,i,n) −v_(2,i,n) )v_(1,i,n) )/(2^(n−2) u^2 )) ⇒s_n =((snu^2 )/(2^(n−2) u^2 )) ⇒s_n =((ns)/2^(n−2) ) total distance ball 1 has traveled till the (n+1)^(th) collision: S_n =s_0 +Σ_(k=1) ^n s_k =s+Σ_(k=1) ^n ((ks)/2^(k−2) ) with s=1 m S_n =1+4Σ_(k=1) ^n (k/2^k ) S_n =1+4(2−((n+2)/2^n )) lim_(n→∞) S_n =1+4×2=9 m that means after a large number of collisions the ball 1 has traveled a total distance of 9 m. the sum of distances between the collisions is 8 m. ■

$${mass}\:{of}\:{the}\:{balls}={m} \\ $$$${force}\:{on}\:{ball}\:\mathrm{1}\:{at}\:{beginning}={f} \\ $$$${distance}\:{between}\:{the}\:{balls}\:{at}\:{beginning}={s}=\mathrm{1} \\ $$$${v}_{\mathrm{1},{i},{n}} ={velocity}\:{of}\:{ball}\:\mathrm{1}\:{before}\:{n}^{{th}} \:{collision} \\ $$$${v}_{\mathrm{1},{f},{n}} ={velocity}\:{of}\:{ball}\:\mathrm{1}\:{after}\:{n}^{{th}} \:{collision} \\ $$$${v}_{\mathrm{2},{i},{n}} ={velocity}\:{of}\:{ball}\:\mathrm{2}\:{before}\:{n}^{{th}} \:{collision} \\ $$$${v}_{\mathrm{2},{f},{n}} ={velocity}\:{of}\:{ball}\:\mathrm{2}\:{after}\:{n}^{{th}} \:{collision} \\ $$$${a}_{{n}} ={acceleration}\:{of}\:{ball}\:\mathrm{1}\:{after}\:{n}^{{th}} \:{collision} \\ $$$${s}_{{n}} ={distance}\:{between}\:{n}^{{th}} \:{and}\:\left({n}+\mathrm{1}\right)^{{th}} \:{collision} \\ $$$$ \\ $$$${as}\:{we}\:{know},\:{after}\:{an}\:{elastic}\:{collision}\: \\ $$$${from}\:{two}\:{balls}\:{with}\:{the}\:{same}\:{mass}\: \\ $$$${they}\:{just}\:{exchange}\:{their}\:{velocities},\:{i}.{e}. \\ $$$${v}_{\mathrm{1},{f},{n}} ={v}_{\mathrm{2},{i},{n}} \\ $$$${v}_{\mathrm{2},{f},{n}} ={v}_{\mathrm{1},{i},{n}} \\ $$$$ \\ $$$$\underline{{before}\:{the}\:\mathrm{1}^{{st}} \:{collision}:} \\ $$$${v}_{\mathrm{2},{i},\mathrm{1}} =\mathrm{0} \\ $$$${a}_{\mathrm{0}} =\frac{{f}}{{m}} \\ $$$${v}_{\mathrm{1},{i},\mathrm{1}} =\sqrt{\mathrm{2}{sa}_{\mathrm{0}} }=\sqrt{\frac{\mathrm{2}{sf}}{{m}}}={u}\:{say} \\ $$$$\:\Rightarrow\frac{{f}}{{m}}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}{s}} \\ $$$$ \\ $$$$\underline{{after}\:{the}\:\mathrm{1}^{{st}} \:{collision}:} \\ $$$${v}_{\mathrm{2},{f},\mathrm{1}} ={v}_{\mathrm{1},{i},\mathrm{1}} ={u} \\ $$$${v}_{\mathrm{1},{f},\mathrm{1}} ={v}_{\mathrm{2},{i},\mathrm{1}} =\mathrm{0} \\ $$$${after}\:{the}\:{collision}\:{the}\:{ball}\:\mathrm{1}\:{gets}\:{a} \\ $$$${force}\:{which}\:{is}\:\mathrm{2}\:{times}\:{of}\:{the}\:{force} \\ $$$${before}\:{the}\:{collision}: \\ $$$${f}_{\mathrm{1}} =\mathrm{2}{f}_{\mathrm{0}} =\mathrm{2}{f} \\ $$$${a}_{\mathrm{1}} =\frac{{f}_{\mathrm{1}} }{{m}}=\frac{\mathrm{2}{f}}{{m}}=\frac{{u}^{\mathrm{2}} }{{s}} \\ $$$${say}\:{after}\:{a}\:{distand}\:{s}_{\mathrm{1}} \:{both}\:{balls} \\ $$$${collide}\:{with}\:{each}\:{other}\:{again}\:{after} \\ $$$${a}\:{time}\:{t}. \\ $$$${s}_{\mathrm{1}} ={v}_{\mathrm{2},{f},\mathrm{1}} {t}={ut} \\ $$$${s}_{\mathrm{1}} ={v}_{\mathrm{1},{f},\mathrm{1}} {t}+\frac{\mathrm{1}}{\mathrm{2}}{a}_{\mathrm{1}} {t}^{\mathrm{2}} \\ $$$${v}_{\mathrm{2},{f},\mathrm{1}} {t}={v}_{\mathrm{1},{f},\mathrm{1}} {t}+\frac{\mathrm{1}}{\mathrm{2}}{a}_{\mathrm{1}} {t}^{\mathrm{2}} \\ $$$${t}=\frac{\mathrm{2}\left({v}_{\mathrm{2},{f},\mathrm{1}} −{v}_{\mathrm{1},{f},\mathrm{1}} \right)}{{a}_{\mathrm{1}} }=\frac{\mathrm{2}{s}\left({u}−\mathrm{0}\right)}{{u}^{\mathrm{2}} }=\frac{\mathrm{2}{s}}{{u}} \\ $$$${s}_{\mathrm{1}} =\frac{\mathrm{2}{s}\left({v}_{\mathrm{2},{f},\mathrm{1}} −{v}_{\mathrm{1},{f},\mathrm{1}} \right)}{{u}}=\frac{\mathrm{2}{s}\left({u}−\mathrm{0}\right)}{{u}}=\mathrm{2}{s} \\ $$$${v}_{\mathrm{2},{i},\mathrm{2}} ={v}_{\mathrm{2},{f},\mathrm{1}} ={u} \\ $$$${v}_{\mathrm{1},{i},\mathrm{2}} ={v}_{\mathrm{1},{f},\mathrm{1}} +{a}_{\mathrm{1}} {t}=\mathrm{0}+\frac{{u}^{\mathrm{2}} }{{s}}×\frac{\mathrm{2}{s}}{{u}}=\mathrm{2}{u} \\ $$$$ \\ $$$$\underline{{after}\:{the}\:{n}^{{th}} \:{collision}:} \\ $$$${v}_{\mathrm{1},{f},{n}} ={v}_{\mathrm{2},{i},{n}} \\ $$$${v}_{\mathrm{2},{f},{n}} ={v}_{\mathrm{1},{i},{n}} \\ $$$${f}_{{n}} =\mathrm{2}^{{n}} {f} \\ $$$${a}_{{n}} =\frac{{f}_{{n}} }{{m}}=\frac{\mathrm{2}^{{n}} {f}}{{m}}=\mathrm{2}^{{n}} ×\frac{{u}^{\mathrm{2}} }{\mathrm{2}{s}}=\frac{\mathrm{2}^{{n}−\mathrm{1}} {u}^{\mathrm{2}} }{{s}} \\ $$$${say}\:{after}\:{a}\:{distance}\:{s}_{{n}} \:{the}\:{both}\:{balls} \\ $$$${collide}\:{with}\:{each}\:{other}\:{again}\:{after} \\ $$$${time}\:{t}. \\ $$$${s}_{{n}} ={v}_{\mathrm{2},{f},{n}} {t} \\ $$$${s}_{{n}} ={v}_{\mathrm{1},{f},{n}} {t}+\frac{\mathrm{1}}{\mathrm{2}}{a}_{{n}} {t}^{\mathrm{2}} \\ $$$${v}_{\mathrm{2},{f},{n}} {t}={v}_{\mathrm{1},{f},{n}} {t}+\frac{\mathrm{1}}{\mathrm{2}}{a}_{{n}} {t}^{\mathrm{2}} \\ $$$${t}=\frac{{s}\left({v}_{\mathrm{2},{f},{n}} −{v}_{\mathrm{1},{f},{n}} \right)}{\mathrm{2}^{{n}−\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$${s}_{{n}} =\frac{{s}\left({v}_{\mathrm{2},{f},{n}} −{v}_{\mathrm{1},{f},{n}} \right){v}_{\mathrm{2},{f},{n}} }{\mathrm{2}^{{n}−\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$${v}_{\mathrm{2},{i},{n}+\mathrm{1}} ={v}_{\mathrm{2},{f},{n}} \\ $$$${v}_{\mathrm{1},{i},{n}+\mathrm{1}} ={v}_{\mathrm{1},{f},{n}} +{a}_{{n}} {t}={v}_{\mathrm{1},{f},{n}} +\frac{\mathrm{2}^{{n}−\mathrm{1}} {u}^{\mathrm{2}} }{{s}}×\frac{{s}\left({v}_{\mathrm{2},{f},{n}} −{v}_{\mathrm{1},{f},{n}} \right)}{\mathrm{2}^{{n}−\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$${v}_{\mathrm{1},{i},{n}+\mathrm{1}} =\mathrm{2}{v}_{\mathrm{2},{f},{n}} −{v}_{\mathrm{1},{f},{n}} \\ $$$${v}_{\mathrm{1},{i},{n}+\mathrm{1}} =\mathrm{2}{v}_{\mathrm{1},{i},{n}} −{v}_{\mathrm{1},{f},{n}} \\ $$$${v}_{\mathrm{1},{i},{n}+\mathrm{1}} =\mathrm{2}{v}_{\mathrm{1},{i},{n}} −{v}_{\mathrm{2},{i},{n}} \\ $$$${v}_{\mathrm{1},{i},{n}+\mathrm{1}} =\mathrm{2}{v}_{\mathrm{1},{i},{n}} −{v}_{\mathrm{2},{f},{n}−\mathrm{1}} \\ $$$${v}_{\mathrm{1},{i},{n}+\mathrm{1}} =\mathrm{2}{v}_{\mathrm{1},{i},{n}} −{v}_{\mathrm{1},{i},{n}−\mathrm{1}} \\ $$$${v}_{\mathrm{1},{i},{n}+\mathrm{1}} −{v}_{\mathrm{1},{i},{n}} ={v}_{\mathrm{1},{i},{n}} −{v}_{\mathrm{1},{i},{n}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={v}_{\mathrm{1},{i},\mathrm{2}} −{v}_{\mathrm{1},{i},\mathrm{1}} =\mathrm{2}{u}−{u}={u} \\ $$$$\Rightarrow{v}_{\mathrm{1},{i},{n}} ={nu} \\ $$$$\Rightarrow{v}_{\mathrm{2},{i},{n}} ={v}_{\mathrm{2},{f},{n}−\mathrm{1}} ={v}_{\mathrm{1},{i},{n}−\mathrm{1}} =\left({n}−\mathrm{1}\right){u} \\ $$$${s}_{{n}} =\frac{{s}\left({v}_{\mathrm{2},{f},{n}} −{v}_{\mathrm{1},{f},{n}} \right){v}_{\mathrm{2},{f},{n}} }{\mathrm{2}^{{n}−\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$${s}_{{n}} =\frac{{s}\left({v}_{\mathrm{1},{i},{n}} −{v}_{\mathrm{2},{i},{n}} \right){v}_{\mathrm{1},{i},{n}} }{\mathrm{2}^{{n}−\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$$\Rightarrow{s}_{{n}} =\frac{{snu}^{\mathrm{2}} }{\mathrm{2}^{{n}−\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$$\Rightarrow{s}_{{n}} =\frac{{ns}}{\mathrm{2}^{{n}−\mathrm{2}} } \\ $$$$ \\ $$$${total}\:{distance}\:{ball}\:\mathrm{1}\:{has}\:{traveled}\:{till} \\ $$$${the}\:\left({n}+\mathrm{1}\right)^{{th}} \:{collision}: \\ $$$${S}_{{n}} ={s}_{\mathrm{0}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{s}_{{k}} ={s}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{ks}}{\mathrm{2}^{{k}−\mathrm{2}} } \\ $$$${with}\:{s}=\mathrm{1}\:{m} \\ $$$${S}_{{n}} =\mathrm{1}+\mathrm{4}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}}{\mathrm{2}^{{k}} } \\ $$$${S}_{{n}} =\mathrm{1}+\mathrm{4}\left(\mathrm{2}−\frac{{n}+\mathrm{2}}{\mathrm{2}^{{n}} }\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}_{{n}} =\mathrm{1}+\mathrm{4}×\mathrm{2}=\mathrm{9}\:{m}\: \\ $$$${that}\:{means}\:{after}\:{a}\:{large}\:{number}\:{of} \\ $$$${collisions}\:{the}\:{ball}\:\mathrm{1}\:{has}\:{traveled}\:{a}\: \\ $$$${total}\:{distance}\:{of}\:\mathrm{9}\:{m}. \\ $$$${the}\:{sum}\:{of}\:{distances}\:{between}\:{the} \\ $$$${collisions}\:{is}\:\mathrm{8}\:{m}. \\ $$$$\blacksquare \\ $$

Commented by mr W last updated on 05/Jan/22

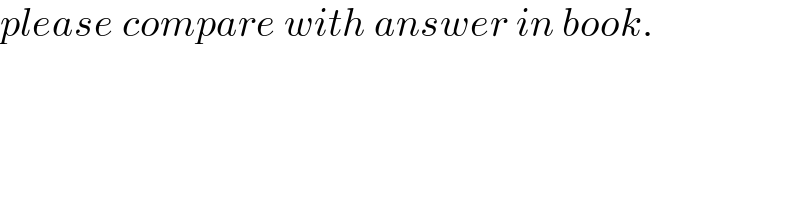
please compare with answer in book.

$${please}\:{compare}\:{with}\:{answer}\:{in}\:{book}. \\ $$

Commented by Tawa11 last updated on 06/Jan/22

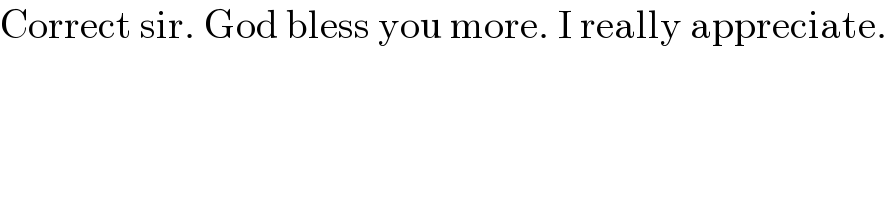
Correct sir. God bless you more. I really appreciate.

$$\mathrm{Correct}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mr W last updated on 06/Jan/22

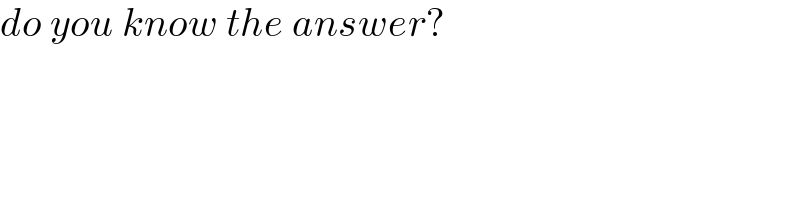
do you know the answer?

$${do}\:{you}\:{know}\:{the}\:{answer}? \\ $$

Commented by Tawa11 last updated on 06/Jan/22

Yes sir. The answer, they wrote 8d at the back of the book sir.

$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{The}\:\mathrm{answer},\:\mathrm{they}\:\mathrm{wrote}\:\:\:\:\mathrm{8d}\:\:\:\mathrm{at}\:\mathrm{the}\:\mathrm{back}\:\mathrm{of}\:\mathrm{the}\:\mathrm{book}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 06/Jan/22

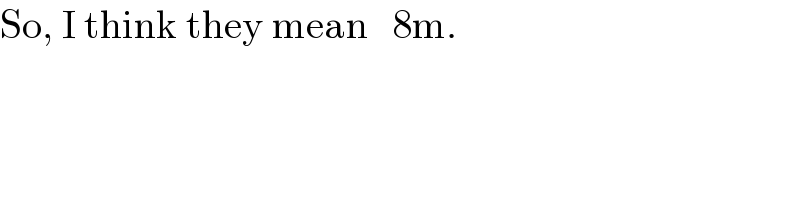
So, I think they mean 8m.

$$\mathrm{So},\:\mathrm{I}\:\mathrm{think}\:\mathrm{they}\:\mathrm{mean}\:\:\:\mathrm{8m}. \\ $$

Commented by mr W last updated on 06/Jan/22

the question says the distance between the balls at t=0 is 1m. if this distance is d (or s in my workings), then the sum of the distances between the collisions is 8d (or 8s in my workings).

$${the}\:{question}\:{says}\:{the}\:{distance}\:{between} \\ $$$${the}\:{balls}\:{at}\:{t}=\mathrm{0}\:{is}\:\mathrm{1}{m}.\:{if}\:{this}\:{distance} \\ $$$${is}\:{d}\:\left({or}\:{s}\:{in}\:{my}\:{workings}\right),\:{then}\:{the} \\ $$$${sum}\:{of}\:{the}\:{distances}\:{between}\:{the} \\ $$$${collisions}\:{is}\:\mathrm{8}{d}\:\left({or}\:\mathrm{8}{s}\:{in}\:{my}\:{workings}\right). \\ $$

Commented by Tawa11 last updated on 06/Jan/22

Yes sir. Thanks for your time.

$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com