Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 162834 by mkam last updated on 01/Jan/22

Answered by abdullahhhhh last updated on 01/Jan/22

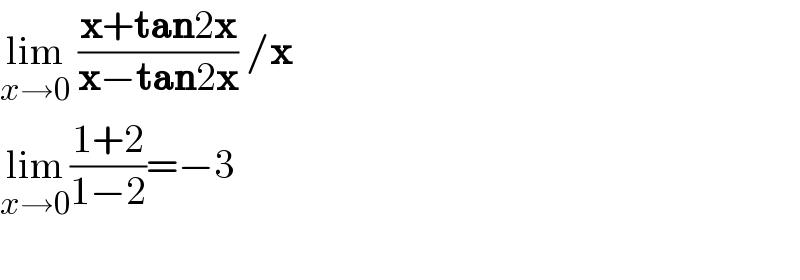
lim_(x→0) ((x+tan2x)/(x−tan2x)) /x lim_(x→0) ((1+2)/(1−2))=−3

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{tan}}\mathrm{2}\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{tan}}\mathrm{2}\boldsymbol{\mathrm{x}}}\:/\boldsymbol{\mathrm{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\mathrm{2}}{\mathrm{1}−\mathrm{2}}=−\mathrm{3} \\ $$$$ \\ $$

Answered by abdullahhhhh last updated on 01/Jan/22

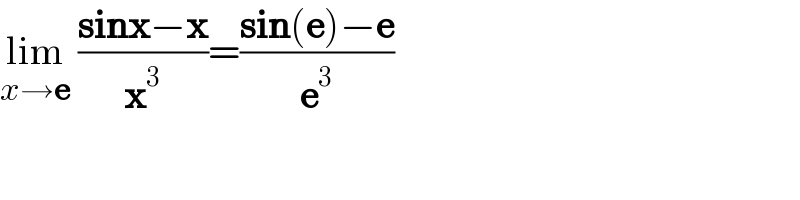
lim_(x→e) ((sinx−x)/x^3 )=((sin(e)−e)/e^3 )

$$\underset{{x}\rightarrow\boldsymbol{\mathrm{e}}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{sinx}}−\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} }=\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{e}}\right)−\boldsymbol{\mathrm{e}}}{\boldsymbol{\mathrm{e}}^{\mathrm{3}} } \\ $$$$ \\ $$

Answered by abdullahhhhh last updated on 01/Jan/22

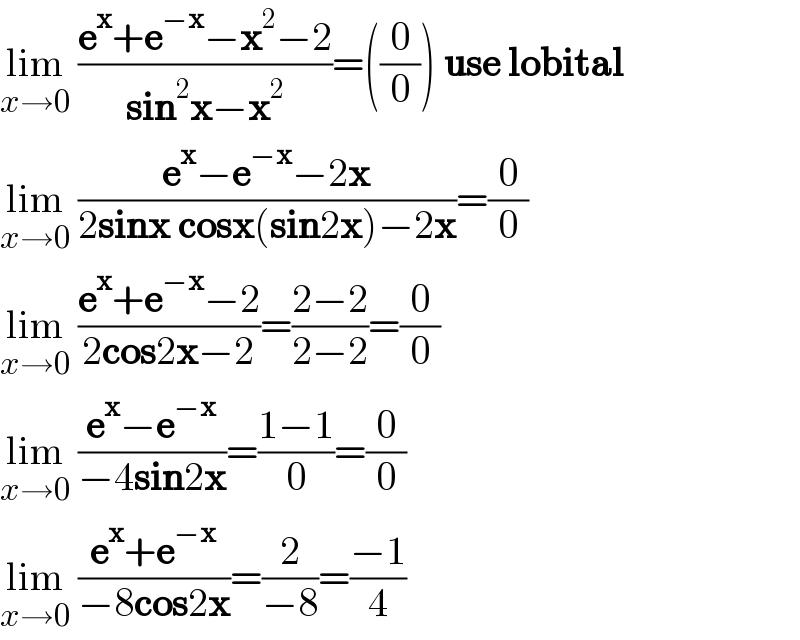
lim_(x→0) ((e^x +e^(−x) −x^2 −2)/(sin^2 x−x^2 ))=((0/0)) use lobital lim_(x→0) ((e^x −e^(−x) −2x)/(2sinx cosx(sin2x)−2x))=(0/0) lim_(x→0) ((e^x +e^(−x) −2)/(2cos2x−2))=((2−2)/(2−2))=(0/0) lim_(x→0) ((e^x −e^(−x) )/(−4sin2x))=((1−1)/0)=(0/0) lim_(x→0) ((e^x +e^(−x) )/(−8cos2x))=(2/(−8))=((−1)/4)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} −\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}}{\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\left(\frac{\mathrm{0}}{\mathrm{0}}\right)\:\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{lobital}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} −\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} −\mathrm{2}\boldsymbol{\mathrm{x}}}{\mathrm{2}\boldsymbol{\mathrm{sinx}}\:\boldsymbol{\mathrm{cosx}}\left(\boldsymbol{\mathrm{sin}}\mathrm{2}\boldsymbol{\mathrm{x}}\right)−\mathrm{2}\boldsymbol{\mathrm{x}}}=\frac{\mathrm{0}}{\mathrm{0}}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} −\mathrm{2}}{\mathrm{2}\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{\mathrm{x}}−\mathrm{2}}=\frac{\mathrm{2}−\mathrm{2}}{\mathrm{2}−\mathrm{2}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} −\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} }{−\mathrm{4}\boldsymbol{\mathrm{sin}}\mathrm{2}\boldsymbol{\mathrm{x}}}=\frac{\mathrm{1}−\mathrm{1}}{\mathrm{0}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} }{−\mathrm{8}\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{\mathrm{x}}}=\frac{\mathrm{2}}{−\mathrm{8}}=\frac{−\mathrm{1}}{\mathrm{4}} \\ $$

Answered by abdullahhhhh last updated on 01/Jan/22

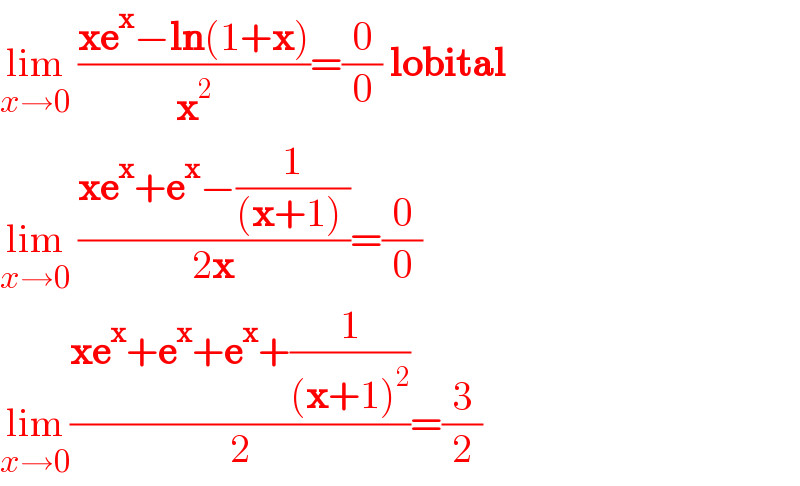
lim_(x→0) ((xe^x −ln(1+x))/x^2 )=(0/0) lobital lim_(x→0) ((xe^x +e^x −(1/((x+1) )))/(2x))=(0/0) lim_(x→0) ((xe^x +e^x +e^x +(1/((x+1)^2 )))/2)=(3/2)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{xe}}^{\boldsymbol{\mathrm{x}}} −\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\frac{\mathrm{0}}{\mathrm{0}}\:\boldsymbol{\mathrm{lobital}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{\mathrm{xe}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} −\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)\:}}{\mathrm{2}\boldsymbol{\mathrm{x}}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{xe}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Answered by abdullahhhhh last updated on 01/Jan/22

lim_(x→∞) (((lnx)/x))=(∞/∞) use lobital lim_(x→∞) (1/x)=(1/∞)=0

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\boldsymbol{\mathrm{lnx}}}{\boldsymbol{\mathrm{x}}}\right)=\frac{\infty}{\infty}\:\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{lobital}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}=\frac{\mathrm{1}}{\infty}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com