Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 162674 by Mathematification last updated on 31/Dec/21

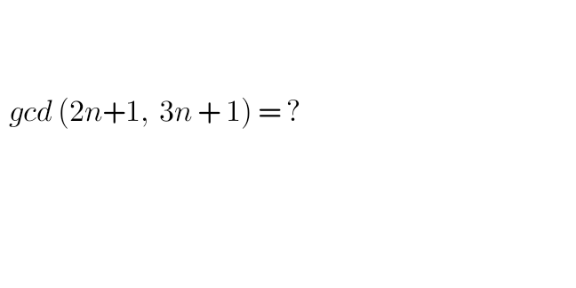
Answered by mindispower last updated on 31/Dec/21

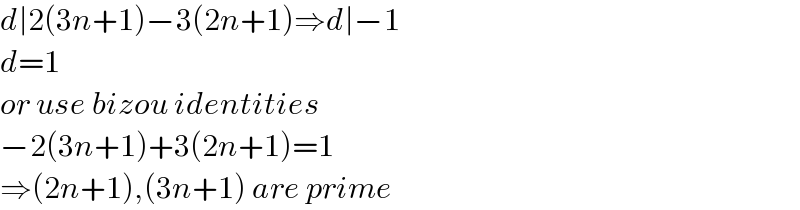
d∣2(3n+1)−3(2n+1)⇒d∣−1 d=1 or use bizou identities −2(3n+1)+3(2n+1)=1 ⇒(2n+1),(3n+1) are prime

$${d}\mid\mathrm{2}\left(\mathrm{3}{n}+\mathrm{1}\right)−\mathrm{3}\left(\mathrm{2}{n}+\mathrm{1}\right)\Rightarrow{d}\mid−\mathrm{1} \\ $$$${d}=\mathrm{1} \\ $$$${or}\:{use}\:{bizou}\:{identities} \\ $$$$−\mathrm{2}\left(\mathrm{3}{n}+\mathrm{1}\right)+\mathrm{3}\left(\mathrm{2}{n}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{2}{n}+\mathrm{1}\right),\left(\mathrm{3}{n}+\mathrm{1}\right)\:{are}\:{prime} \\ $$

Answered by mr W last updated on 31/Dec/21

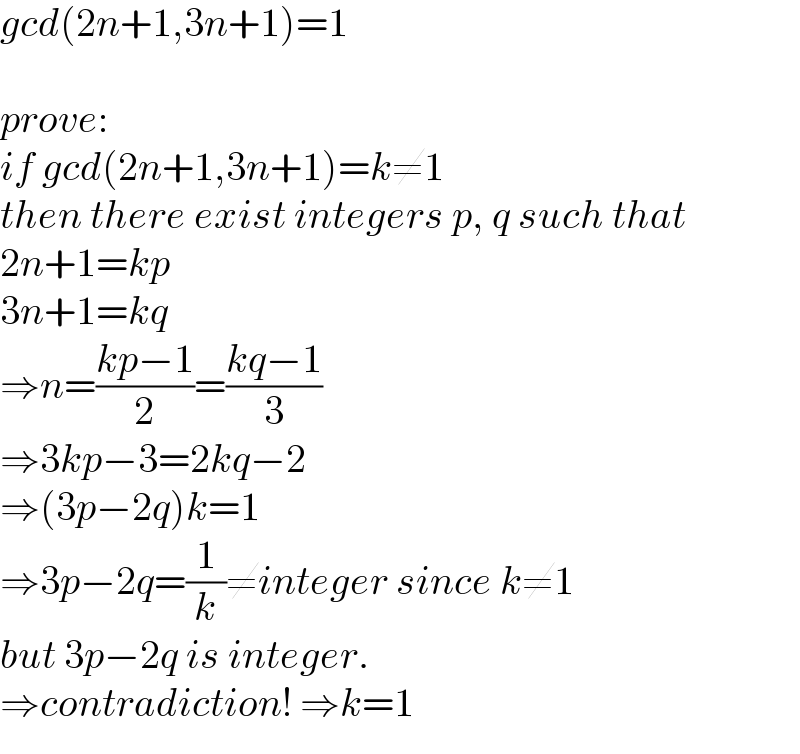
gcd(2n+1,3n+1)=1 prove: if gcd(2n+1,3n+1)=k≠1 then there exist integers p, q such that 2n+1=kp 3n+1=kq ⇒n=((kp−1)/2)=((kq−1)/3) ⇒3kp−3=2kq−2 ⇒(3p−2q)k=1 ⇒3p−2q=(1/k)≠integer since k≠1 but 3p−2q is integer. ⇒contradiction! ⇒k=1

$${gcd}\left(\mathrm{2}{n}+\mathrm{1},\mathrm{3}{n}+\mathrm{1}\right)=\mathrm{1} \\ $$$$ \\ $$$${prove}: \\ $$$${if}\:{gcd}\left(\mathrm{2}{n}+\mathrm{1},\mathrm{3}{n}+\mathrm{1}\right)={k}\neq\mathrm{1} \\ $$$${then}\:{there}\:{exist}\:{integers}\:{p},\:{q}\:{such}\:{that} \\ $$$$\mathrm{2}{n}+\mathrm{1}={kp} \\ $$$$\mathrm{3}{n}+\mathrm{1}={kq} \\ $$$$\Rightarrow{n}=\frac{{kp}−\mathrm{1}}{\mathrm{2}}=\frac{{kq}−\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}{kp}−\mathrm{3}=\mathrm{2}{kq}−\mathrm{2} \\ $$$$\Rightarrow\left(\mathrm{3}{p}−\mathrm{2}{q}\right){k}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}{p}−\mathrm{2}{q}=\frac{\mathrm{1}}{{k}}\neq{integer}\:{since}\:{k}\neq\mathrm{1} \\ $$$${but}\:\mathrm{3}{p}−\mathrm{2}{q}\:{is}\:{integer}.\: \\ $$$$\Rightarrow{contradiction}!\:\Rightarrow{k}=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com