
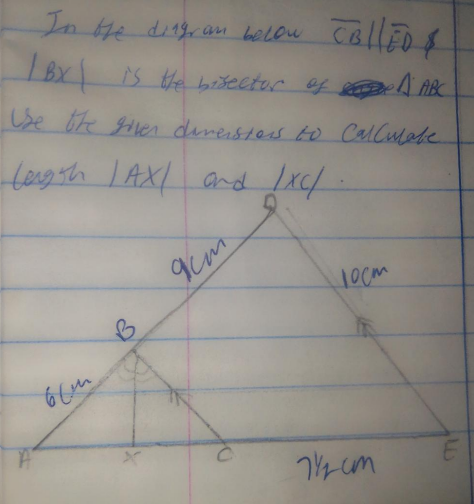
Question Number 161866 by Tawa11 last updated on 23/Dec/21
Commented by mr W last updated on 23/Dec/21
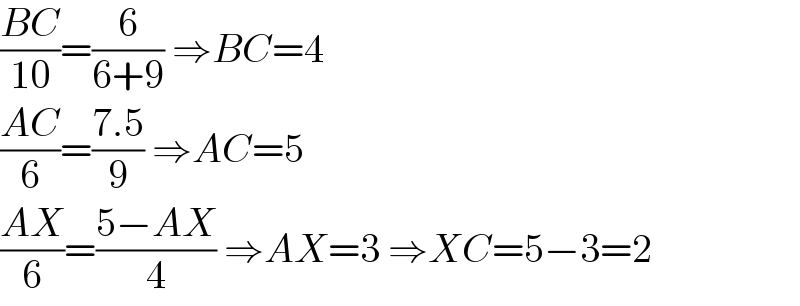
$$\frac{{BC}}{\mathrm{10}}=\frac{\mathrm{6}}{\mathrm{6}+\mathrm{9}}\:\Rightarrow{BC}=\mathrm{4} \\ $$$$\frac{{AC}}{\mathrm{6}}=\frac{\mathrm{7}.\mathrm{5}}{\mathrm{9}}\:\Rightarrow{AC}=\mathrm{5} \\ $$$$\frac{{AX}}{\mathrm{6}}=\frac{\mathrm{5}−{AX}}{\mathrm{4}}\:\Rightarrow{AX}=\mathrm{3}\:\Rightarrow{XC}=\mathrm{5}−\mathrm{3}=\mathrm{2} \\ $$
Commented by Tawa11 last updated on 23/Dec/21

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now}. \\ $$
Commented by mr W last updated on 23/Dec/21

$${it}'{s}\:{fine}\:{when}\:{you}\:{understand}\:{now}. \\ $$
Answered by som(math1967) last updated on 23/Dec/21
![((AB)/(AD))=((BC)/(DE)) [BC∥DE ∴ △ABC∼△ADE] (6/(15))=((BC)/(10))⇒BC=4cm again BC∥DE ∴((AB)/(BD))=((AC)/(CE)) (6/9)=((AC)/(7.5)) ⇒AC=5cm BX is bisector of ∠ABC ∴((AX)/(XC))=((AB)/(BC))=(6/4)=(3/2) ∴ AX:XC=3:2 AC=5cm ∴AX=(3/5)×5=3cm ans XC=(2/5)×5=2cm ans](Q161877.png)
$$\frac{{AB}}{{AD}}=\frac{{BC}}{{DE}}\:\:\:\:\left[{BC}\parallel{DE}\:\therefore\:\bigtriangleup{ABC}\sim\bigtriangleup{ADE}\right] \\ $$$$\frac{\mathrm{6}}{\mathrm{15}}=\frac{{BC}}{\mathrm{10}}\Rightarrow{BC}=\mathrm{4}{cm} \\ $$$${again}\:{BC}\parallel{DE} \\ $$$$\therefore\frac{{AB}}{{BD}}=\frac{{AC}}{{CE}} \\ $$$$\:\frac{\mathrm{6}}{\mathrm{9}}=\frac{{AC}}{\mathrm{7}.\mathrm{5}}\:\:\Rightarrow{AC}=\mathrm{5}{cm} \\ $$$${BX}\:{is}\:{bisector}\:{of}\:\angle{ABC} \\ $$$$\therefore\frac{{AX}}{{XC}}=\frac{{AB}}{{BC}}=\frac{\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\therefore\:{AX}:{XC}=\mathrm{3}:\mathrm{2} \\ $$$${AC}=\mathrm{5}{cm} \\ $$$$\therefore{AX}=\frac{\mathrm{3}}{\mathrm{5}}×\mathrm{5}=\mathrm{3}{cm}\:{ans} \\ $$$${XC}=\frac{\mathrm{2}}{\mathrm{5}}×\mathrm{5}=\mathrm{2}{cm}\:\:{ans} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 23/Dec/21

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
