Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 161241 by help last updated on 14/Dec/21

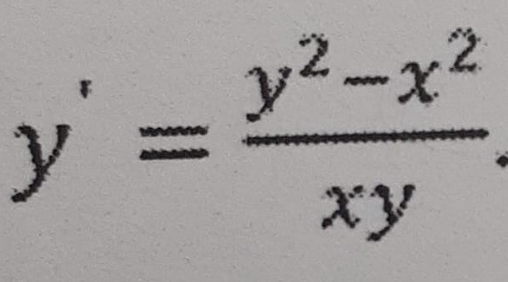
Answered by mr W last updated on 15/Dec/21

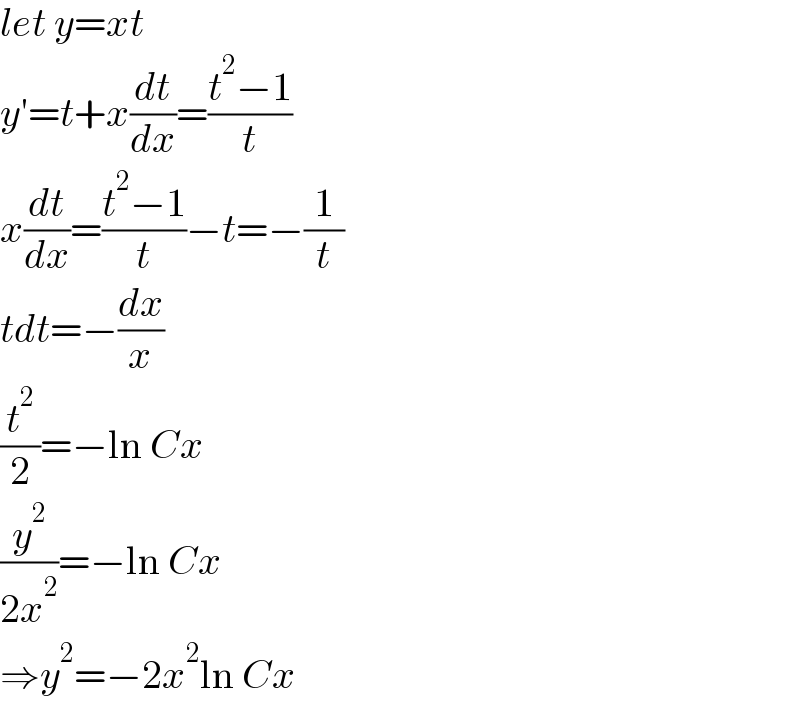
let y=xt y′=t+x(dt/dx)=((t^2 −1)/t) x(dt/dx)=((t^2 −1)/t)−t=−(1/t) tdt=−(dx/x) (t^2 /2)=−ln Cx (y^2 /(2x^2 ))=−ln Cx ⇒y^2 =−2x^2 ln Cx

$${let}\:{y}={xt} \\ $$$${y}'={t}+{x}\frac{{dt}}{{dx}}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}} \\ $$$${x}\frac{{dt}}{{dx}}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}}−{t}=−\frac{\mathrm{1}}{{t}} \\ $$$${tdt}=−\frac{{dx}}{{x}} \\ $$$$\frac{{t}^{\mathrm{2}} }{\mathrm{2}}=−\mathrm{ln}\:{Cx} \\ $$$$\frac{{y}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }=−\mathrm{ln}\:{Cx} \\ $$$$\Rightarrow{y}^{\mathrm{2}} =−\mathrm{2}{x}^{\mathrm{2}} \mathrm{ln}\:{Cx} \\ $$

Answered by yeti123 last updated on 15/Dec/21

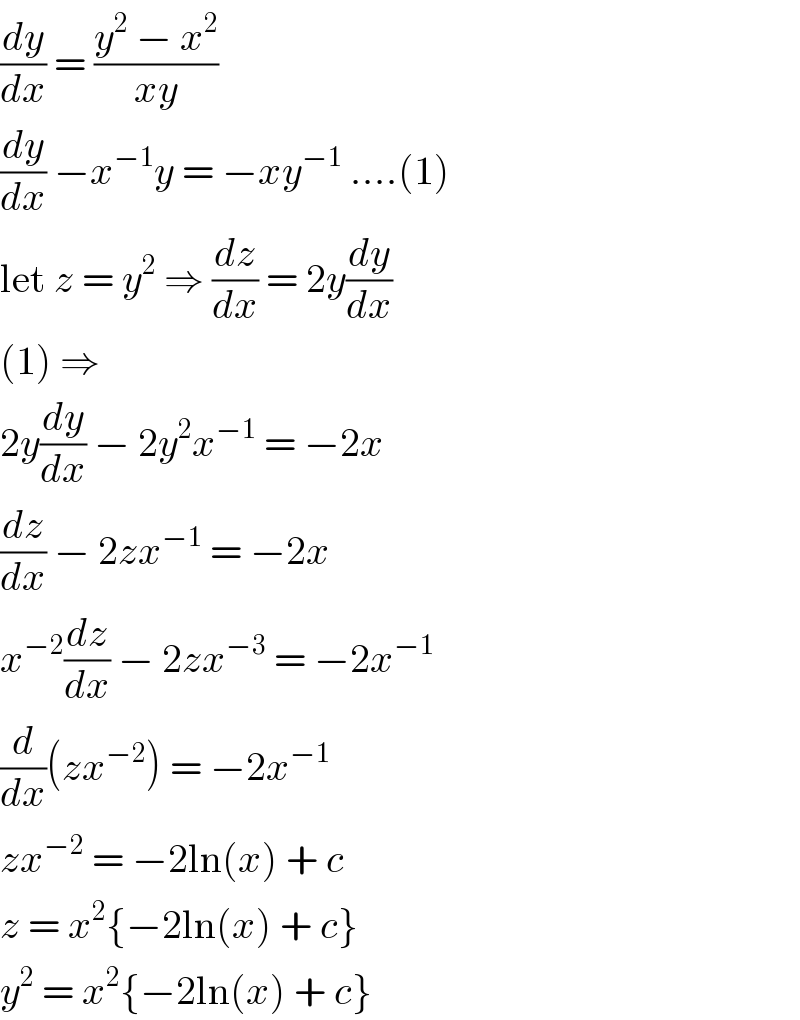
(dy/dx) = ((y^2 − x^2 )/(xy)) (dy/dx) −x^(−1) y = −xy^(−1) ....(1) let z = y^2 ⇒ (dz/dx) = 2y(dy/dx) (1) ⇒ 2y(dy/dx) − 2y^2 x^(−1) = −2x (dz/dx) − 2zx^(−1) = −2x x^(−2) (dz/dx) − 2zx^(−3) = −2x^(−1) (d/dx)(zx^(−2) ) = −2x^(−1) zx^(−2) = −2ln(x) + c z = x^2 {−2ln(x) + c} y^2 = x^2 {−2ln(x) + c}

$$\frac{{dy}}{{dx}}\:=\:\frac{{y}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} }{{xy}} \\ $$$$\frac{{dy}}{{dx}}\:−{x}^{−\mathrm{1}} {y}\:=\:−{xy}^{−\mathrm{1}} \:....\left(\mathrm{1}\right) \\ $$$$\mathrm{let}\:{z}\:=\:{y}^{\mathrm{2}} \:\Rightarrow\:\frac{{dz}}{{dx}}\:=\:\mathrm{2}{y}\frac{{dy}}{{dx}} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{2}{y}\frac{{dy}}{{dx}}\:−\:\mathrm{2}{y}^{\mathrm{2}} {x}^{−\mathrm{1}} \:=\:−\mathrm{2}{x} \\ $$$$\frac{{dz}}{{dx}}\:−\:\mathrm{2}{zx}^{−\mathrm{1}} \:=\:−\mathrm{2}{x} \\ $$$${x}^{−\mathrm{2}} \frac{{dz}}{{dx}}\:−\:\mathrm{2}{zx}^{−\mathrm{3}} \:=\:−\mathrm{2}{x}^{−\mathrm{1}} \\ $$$$\frac{{d}}{{dx}}\left({zx}^{−\mathrm{2}} \right)\:=\:−\mathrm{2}{x}^{−\mathrm{1}} \\ $$$${zx}^{−\mathrm{2}} \:=\:−\mathrm{2ln}\left({x}\right)\:+\:{c} \\ $$$${z}\:=\:{x}^{\mathrm{2}} \left\{−\mathrm{2ln}\left({x}\right)\:+\:{c}\right\} \\ $$$${y}^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} \left\{−\mathrm{2ln}\left({x}\right)\:+\:{c}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com