
Question Number 160317 by quvonnn last updated on 27/Nov/21
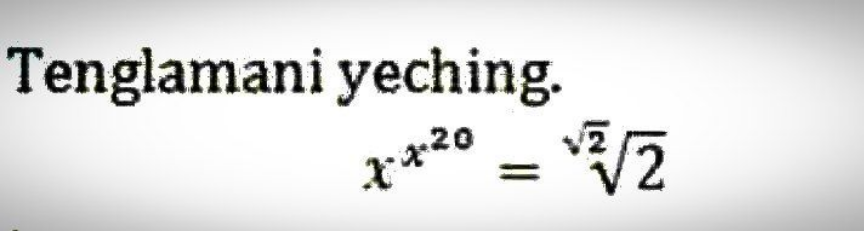
Commented by quvonnn last updated on 27/Nov/21

$$\boldsymbol{{x}}=? \\ $$
Answered by MathsFan last updated on 27/Nov/21
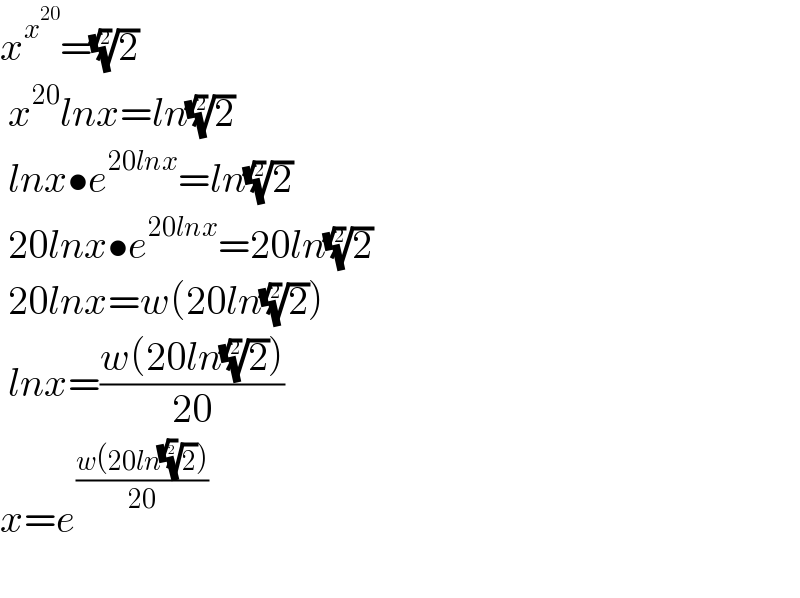
$${x}^{{x}^{\mathrm{20}} } =\sqrt[{\sqrt{\mathrm{2}}}]{\mathrm{2}} \\ $$$$\:{x}^{\mathrm{20}} {lnx}={ln}\sqrt[{\sqrt{\mathrm{2}}}]{\mathrm{2}} \\ $$$$\:{lnx}\bullet{e}^{\mathrm{20}{lnx}} ={ln}\sqrt[{\sqrt{\mathrm{2}}}]{\mathrm{2}} \\ $$$$\:\mathrm{20}{lnx}\bullet{e}^{\mathrm{20}{lnx}} =\mathrm{20}{ln}\sqrt[{\sqrt{\mathrm{2}}}]{\mathrm{2}} \\ $$$$\:\mathrm{20}{lnx}={w}\left(\mathrm{20}{ln}\sqrt[{\sqrt{\mathrm{2}}}]{\mathrm{2}}\right) \\ $$$$\:{lnx}=\frac{{w}\left(\mathrm{20}{ln}\sqrt[{\sqrt{\mathrm{2}}}]{\mathrm{2}}\right)}{\mathrm{20}} \\ $$$${x}={e}^{\frac{{w}\left(\mathrm{20}{ln}\sqrt[{\sqrt{\mathrm{2}}}]{\mathrm{2}}\right)}{\mathrm{20}}} \\ $$$$ \\ $$
Commented by quvonnn last updated on 27/Nov/21

$$\boldsymbol{{w}}=? \\ $$
Commented by quvonnn last updated on 28/Nov/21

$${You}\:{understand} \\ $$
Commented by quvonnn last updated on 28/Nov/21

$${w}=????\:{what} \\ $$
Commented by quvonnn last updated on 28/Nov/21
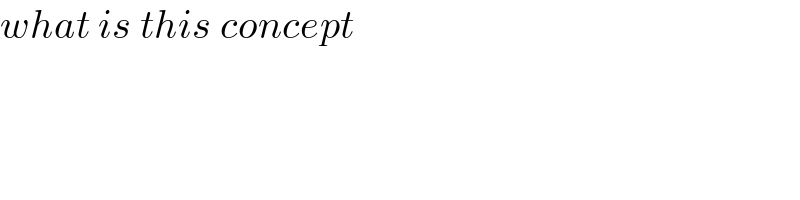
$${what}\:{is}\:{this}\:{concept} \\ $$
Commented by quvonnn last updated on 28/Nov/21
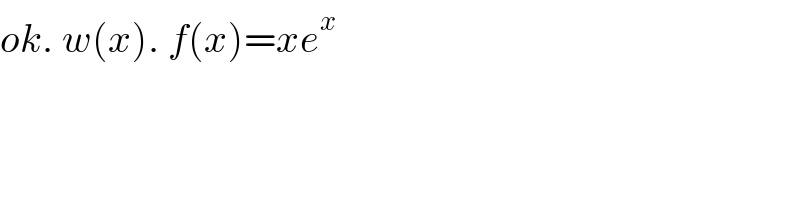
$${ok}.\:{w}\left({x}\right).\:{f}\left({x}\right)={xe}^{{x}} \\ $$
Commented by mr W last updated on 28/Nov/21
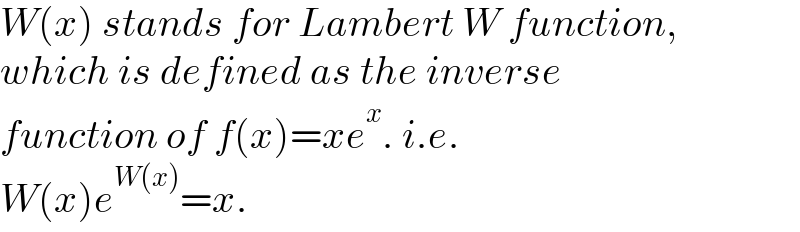
$${W}\left({x}\right)\:{stands}\:{for}\:{Lambert}\:{W}\:{function}, \\ $$$${which}\:{is}\:{defined}\:{as}\:{the}\:{inverse} \\ $$$${function}\:{of}\:{f}\left({x}\right)={xe}^{{x}} .\:{i}.{e}. \\ $$$${W}\left({x}\right){e}^{{W}\left({x}\right)} ={x}. \\ $$
