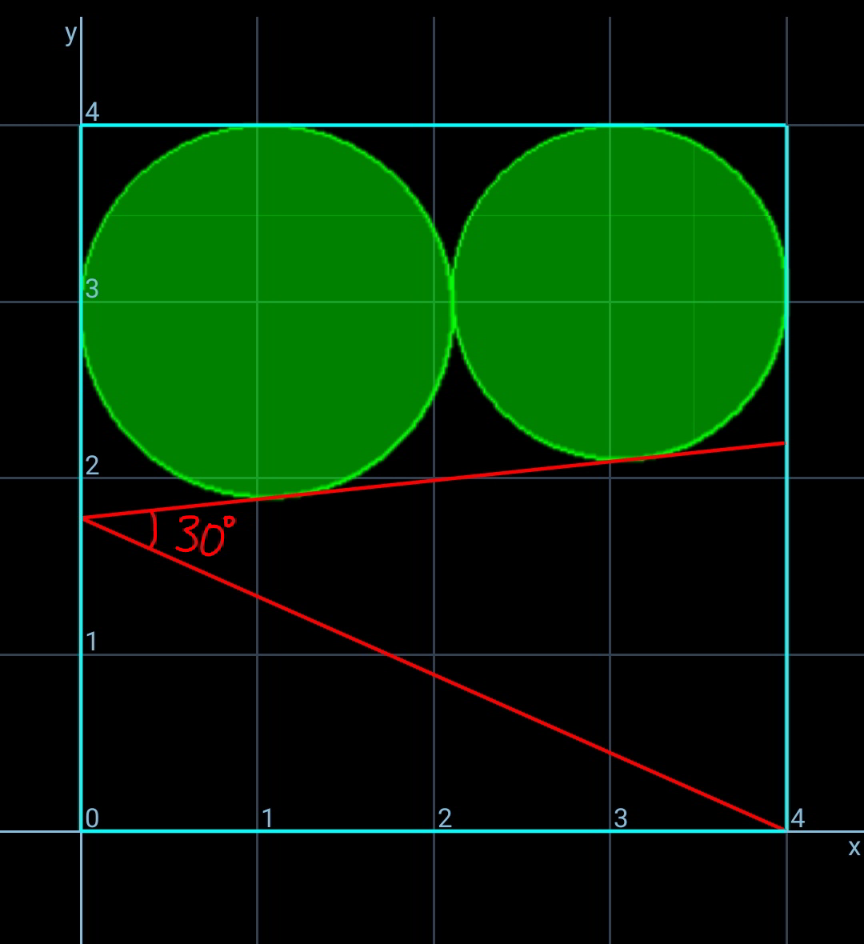
Question Number 159911 by amin96 last updated on 22/Nov/21

Answered by mr W last updated on 22/Nov/21
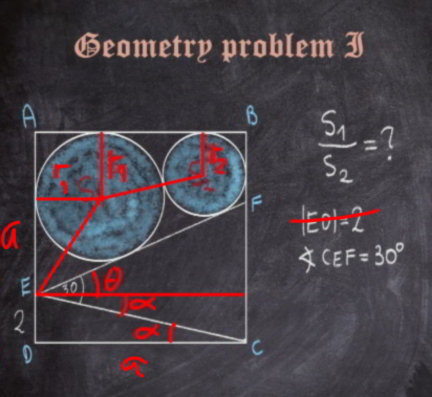
Commented by mr W last updated on 22/Nov/21
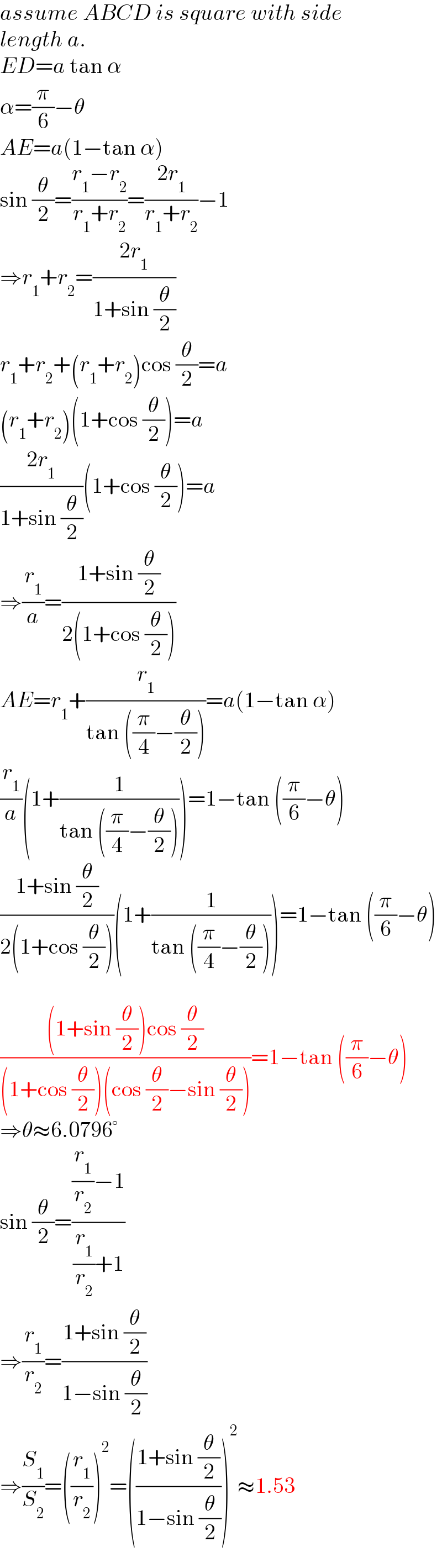
$${assume}\:{ABCD}\:{is}\:{square}\:{with}\:{side} \\ $$$${length}\:{a}. \\ $$$${ED}={a}\:\mathrm{tan}\:\alpha \\ $$$$\alpha=\frac{\pi}{\mathrm{6}}−\theta \\ $$$${AE}={a}\left(\mathrm{1}−\mathrm{tan}\:\alpha\right) \\ $$$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{{r}_{\mathrm{1}} −{r}_{\mathrm{2}} }{{r}_{\mathrm{1}} +{r}_{\mathrm{2}} }=\frac{\mathrm{2}{r}_{\mathrm{1}} }{{r}_{\mathrm{1}} +{r}_{\mathrm{2}} }−\mathrm{1} \\ $$$$\Rightarrow{r}_{\mathrm{1}} +{r}_{\mathrm{2}} =\frac{\mathrm{2}{r}_{\mathrm{1}} }{\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}} \\ $$$${r}_{\mathrm{1}} +{r}_{\mathrm{2}} +\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)\mathrm{cos}\:\frac{\theta}{\mathrm{2}}={a} \\ $$$$\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)={a} \\ $$$$\frac{\mathrm{2}{r}_{\mathrm{1}} }{\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\left(\mathrm{1}+\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)={a} \\ $$$$\Rightarrow\frac{{r}_{\mathrm{1}} }{{a}}=\frac{\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)} \\ $$$${AE}={r}_{\mathrm{1}} +\frac{{r}_{\mathrm{1}} }{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)}={a}\left(\mathrm{1}−\mathrm{tan}\:\alpha\right) \\ $$$$\frac{{r}_{\mathrm{1}} }{{a}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)}\right)=\mathrm{1}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{6}}−\theta\right) \\ $$$$\frac{\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)}\right)=\mathrm{1}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{6}}−\theta\right) \\ $$$$ \\ $$$$\frac{\left(\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}{\left(\mathrm{1}+\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right)}=\mathrm{1}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{6}}−\theta\right) \\ $$$$\Rightarrow\theta\approx\mathrm{6}.\mathrm{0796}° \\ $$$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }−\mathrm{1}}{\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }+\mathrm{1}} \\ $$$$\Rightarrow\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }=\frac{\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{sin}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\Rightarrow\frac{{S}_{\mathrm{1}} }{{S}_{\mathrm{2}} }=\left(\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\right)^{\mathrm{2}} \approx\mathrm{1}.\mathrm{53} \\ $$
Commented by Tawa11 last updated on 22/Nov/21

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 22/Nov/21