Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 159864 by cherokeesay last updated on 21/Nov/21

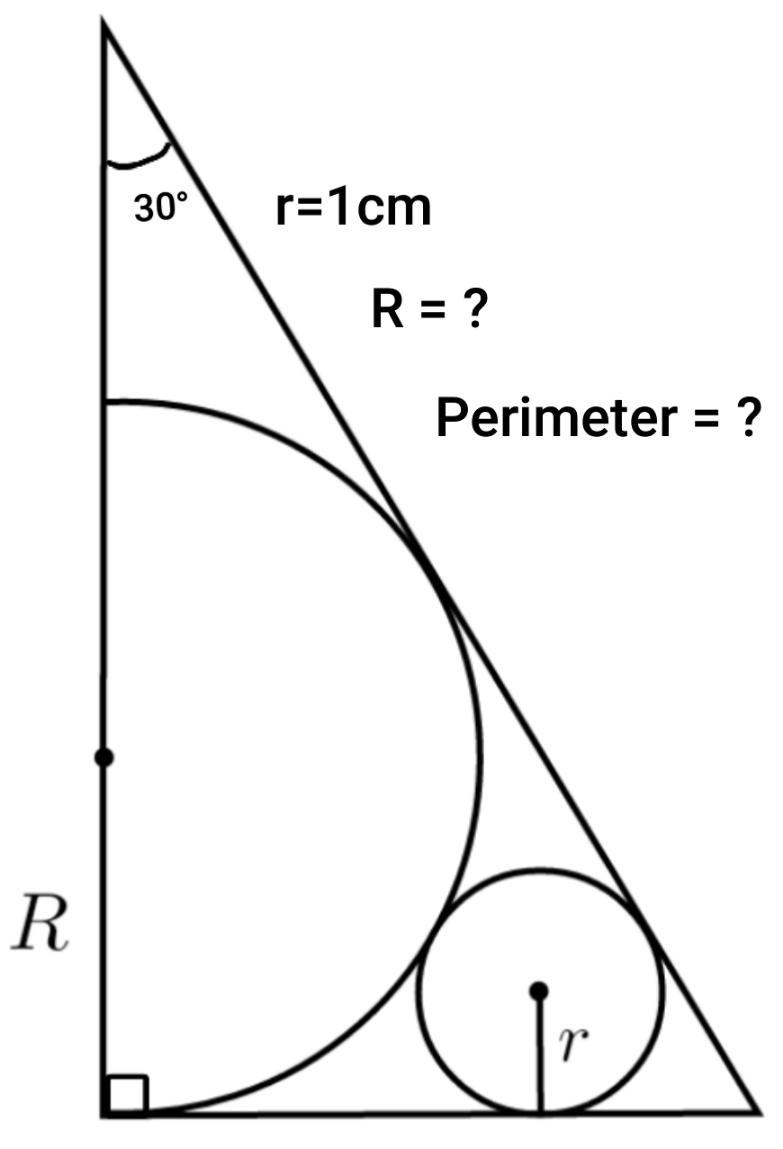
Answered by som(math1967) last updated on 22/Nov/21

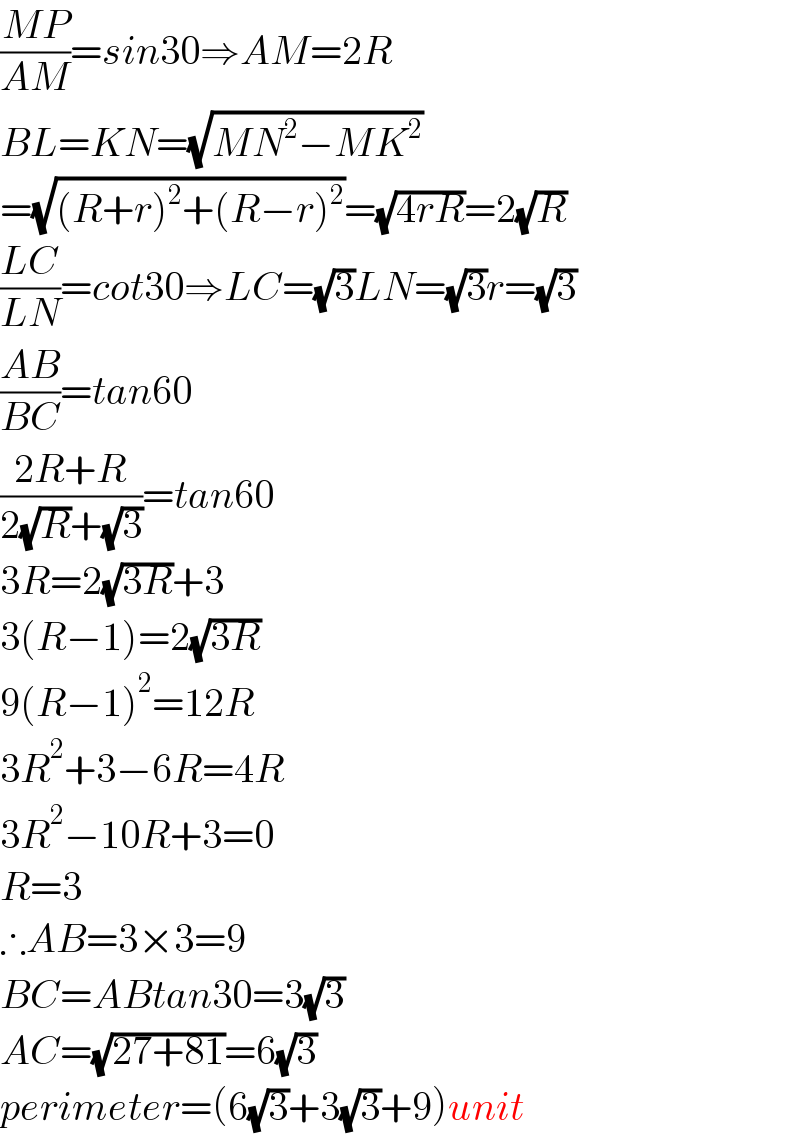
((MP)/(AM))=sin30⇒AM=2R BL=KN=(√(MN^2 −MK^2 )) =(√((R+r)^2 +(R−r)^2 ))=(√(4rR))=2(√R) ((LC)/(LN))=cot30⇒LC=(√3)LN=(√3)r=(√3) ((AB)/(BC))=tan60 ((2R+R)/(2(√R)+(√3)))=tan60 3R=2(√(3R))+3 3(R−1)=2(√(3R)) 9(R−1)^2 =12R 3R^2 +3−6R=4R 3R^2 −10R+3=0 R=3 ∴AB=3×3=9 BC=ABtan30=3(√3) AC=(√(27+81))=6(√3) perimeter=(6(√3)+3(√3)+9)unit

$$\frac{{MP}}{{AM}}={sin}\mathrm{30}\Rightarrow{AM}=\mathrm{2}{R} \\ $$$${BL}={KN}=\sqrt{{MN}^{\mathrm{2}} −{MK}^{\mathrm{2}} } \\ $$$$=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} }=\sqrt{\mathrm{4}{rR}}=\mathrm{2}\sqrt{{R}} \\ $$$$\frac{{LC}}{{LN}}={cot}\mathrm{30}\Rightarrow{LC}=\sqrt{\mathrm{3}}{LN}=\sqrt{\mathrm{3}}{r}=\sqrt{\mathrm{3}} \\ $$$$\frac{{AB}}{{BC}}={tan}\mathrm{60} \\ $$$$\frac{\mathrm{2}{R}+{R}}{\mathrm{2}\sqrt{{R}}+\sqrt{\mathrm{3}}}={tan}\mathrm{60} \\ $$$$\mathrm{3}{R}=\mathrm{2}\sqrt{\mathrm{3}{R}}+\mathrm{3} \\ $$$$\mathrm{3}\left({R}−\mathrm{1}\right)=\mathrm{2}\sqrt{\mathrm{3}{R}} \\ $$$$\mathrm{9}\left({R}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{12}{R} \\ $$$$\mathrm{3}{R}^{\mathrm{2}} +\mathrm{3}−\mathrm{6}{R}=\mathrm{4}{R} \\ $$$$\mathrm{3}{R}^{\mathrm{2}} −\mathrm{10}{R}+\mathrm{3}=\mathrm{0} \\ $$$${R}=\mathrm{3} \\ $$$$\therefore{AB}=\mathrm{3}×\mathrm{3}=\mathrm{9} \\ $$$${BC}={ABtan}\mathrm{30}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${AC}=\sqrt{\mathrm{27}+\mathrm{81}}=\mathrm{6}\sqrt{\mathrm{3}} \\ $$$${perimeter}=\left(\mathrm{6}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{9}\right){unit} \\ $$

Commented by som(math1967) last updated on 22/Nov/21

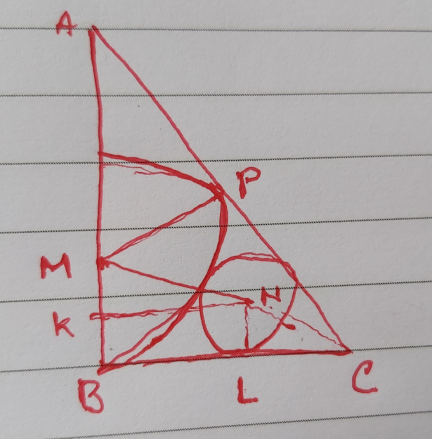
Commented by cherokeesay last updated on 22/Nov/21

thank you sir !

$${thank}\:{you}\:{sir}\:! \\ $$

Answered by mr W last updated on 22/Nov/21

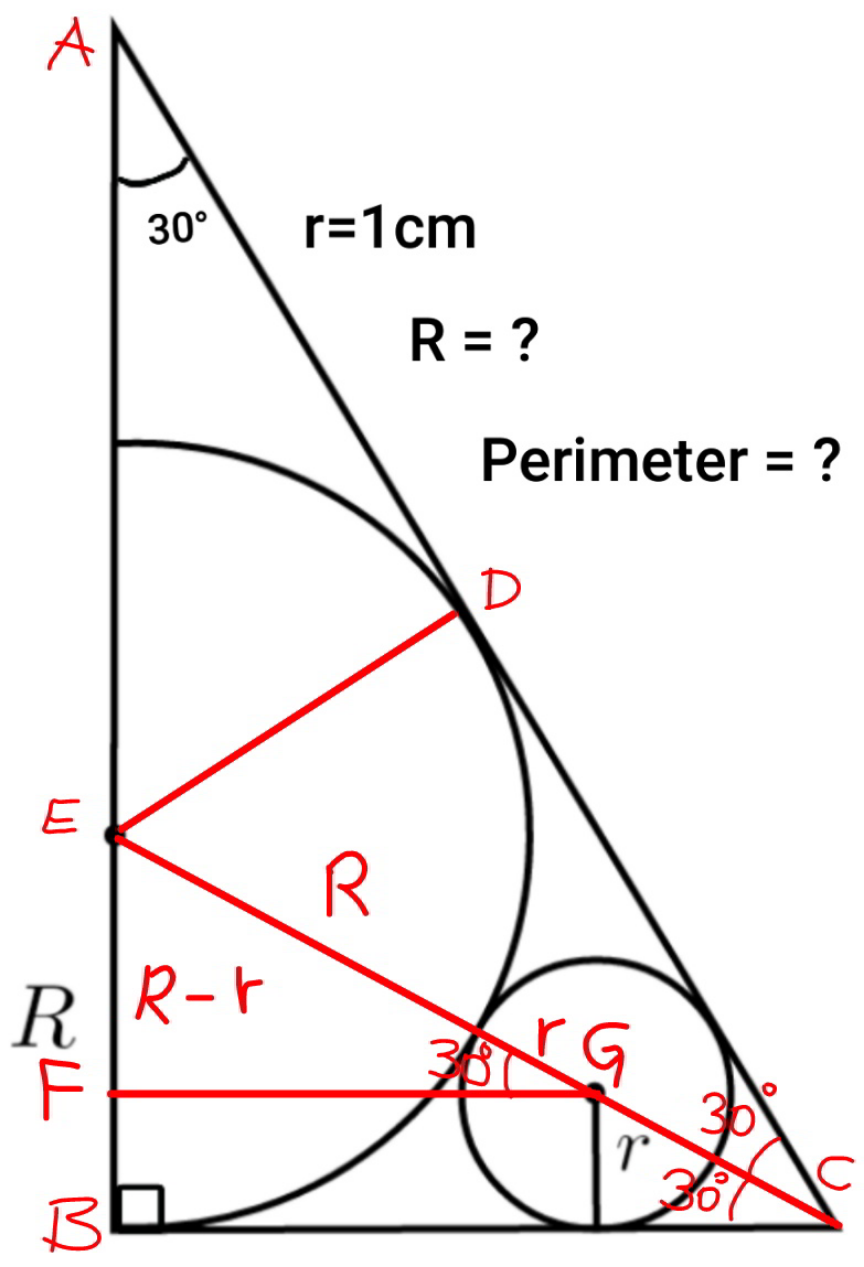
Commented by mr W last updated on 22/Nov/21

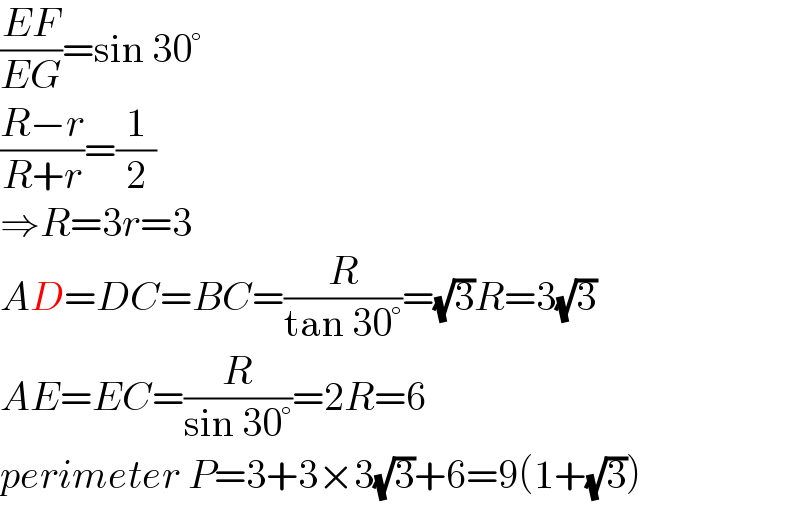
((EF)/(EG))=sin 30° ((R−r)/(R+r))=(1/2) ⇒R=3r=3 AD=DC=BC=(R/(tan 30°))=(√3)R=3(√3) AE=EC=(R/(sin 30°))=2R=6 perimeter P=3+3×3(√3)+6=9(1+(√3))

$$\frac{{EF}}{{EG}}=\mathrm{sin}\:\mathrm{30}° \\ $$$$\frac{{R}−{r}}{{R}+{r}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{R}=\mathrm{3}{r}=\mathrm{3} \\ $$$${AD}={DC}={BC}=\frac{{R}}{\mathrm{tan}\:\mathrm{30}°}=\sqrt{\mathrm{3}}{R}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${AE}={EC}=\frac{{R}}{\mathrm{sin}\:\mathrm{30}°}=\mathrm{2}{R}=\mathrm{6} \\ $$$${perimeter}\:{P}=\mathrm{3}+\mathrm{3}×\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{6}=\mathrm{9}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$

Commented by som(math1967) last updated on 22/Nov/21

Good way sir

$${Good}\:{way}\:{sir} \\ $$

Commented by cherokeesay last updated on 22/Nov/21

very nice ! thank you !

$${very}\:{nice}\:! \\ $$$${thank}\:{you}\:! \\ $$

Commented by Tawa11 last updated on 22/Nov/21

Great

$$\mathrm{Great} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com