
Question Number 159755 by puissant last updated on 20/Nov/21
Commented by puissant last updated on 20/Nov/21
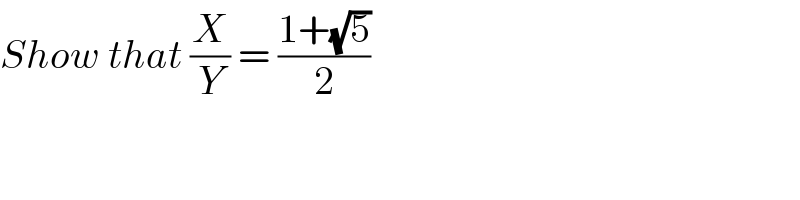
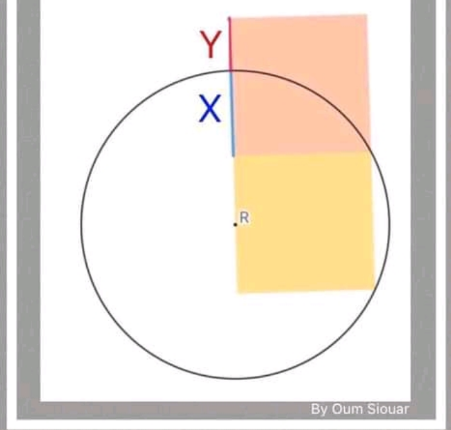
$${Show}\:{that}\:\frac{{X}}{{Y}}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 21/Nov/21
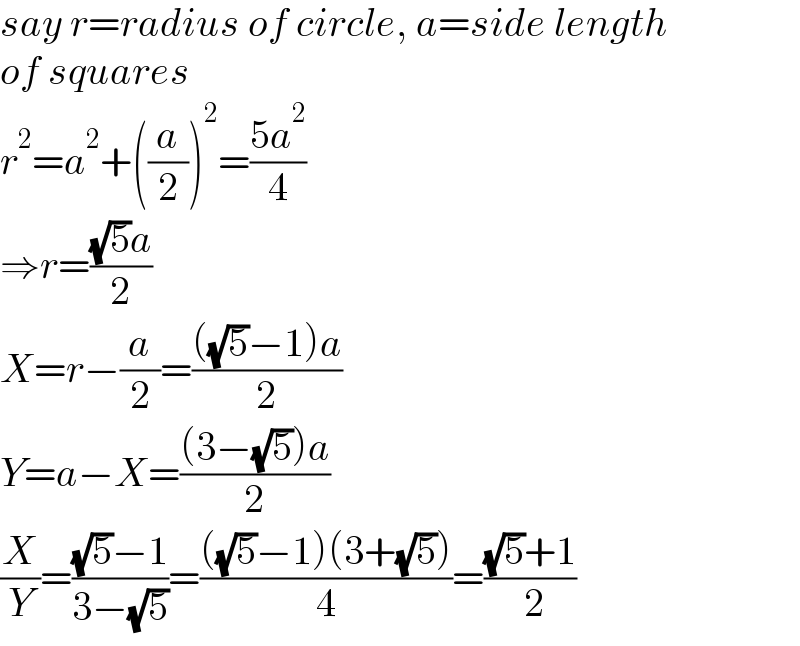
$${say}\:{r}={radius}\:{of}\:{circle},\:{a}={side}\:{length} \\ $$$${of}\:{squares} \\ $$$${r}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{5}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{5}}{a}}{\mathrm{2}} \\ $$$${X}={r}−\frac{{a}}{\mathrm{2}}=\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right){a}}{\mathrm{2}} \\ $$$${Y}={a}−{X}=\frac{\left(\mathrm{3}−\sqrt{\mathrm{5}}\right){a}}{\mathrm{2}} \\ $$$$\frac{{X}}{{Y}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{3}−\sqrt{\mathrm{5}}}=\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)}{\mathrm{4}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\:\mathrm{2}} \\ $$
