Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 159507 by cortano last updated on 18/Nov/21

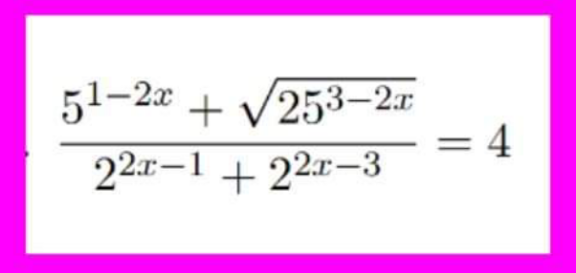
Commented by tounghoungko last updated on 18/Nov/21

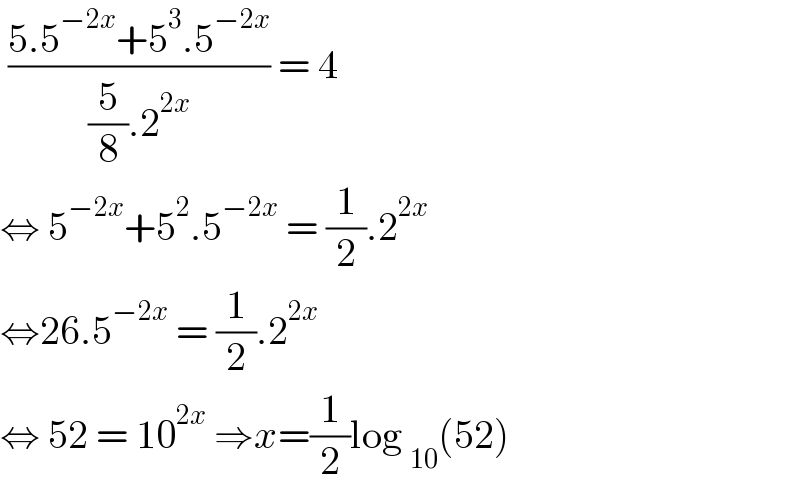
((5.5^(−2x) +5^3 .5^(−2x) )/((5/8).2^(2x) )) = 4 ⇔ 5^(−2x) +5^2 .5^(−2x) = (1/2).2^(2x) ⇔26.5^(−2x) = (1/2).2^(2x) ⇔ 52 = 10^(2x) ⇒x=(1/2)log _(10) (52)

$$\:\frac{\mathrm{5}.\mathrm{5}^{−\mathrm{2}{x}} +\mathrm{5}^{\mathrm{3}} .\mathrm{5}^{−\mathrm{2}{x}} }{\frac{\mathrm{5}}{\mathrm{8}}.\mathrm{2}^{\mathrm{2}{x}} }\:=\:\mathrm{4} \\ $$$$\Leftrightarrow\:\mathrm{5}^{−\mathrm{2}{x}} +\mathrm{5}^{\mathrm{2}} .\mathrm{5}^{−\mathrm{2}{x}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}^{\mathrm{2}{x}} \\ $$$$\Leftrightarrow\mathrm{26}.\mathrm{5}^{−\mathrm{2}{x}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}^{\mathrm{2}{x}} \\ $$$$\Leftrightarrow\:\mathrm{52}\:=\:\mathrm{10}^{\mathrm{2}{x}} \:\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{52}\right) \\ $$

Answered by Tokugami last updated on 18/Nov/21

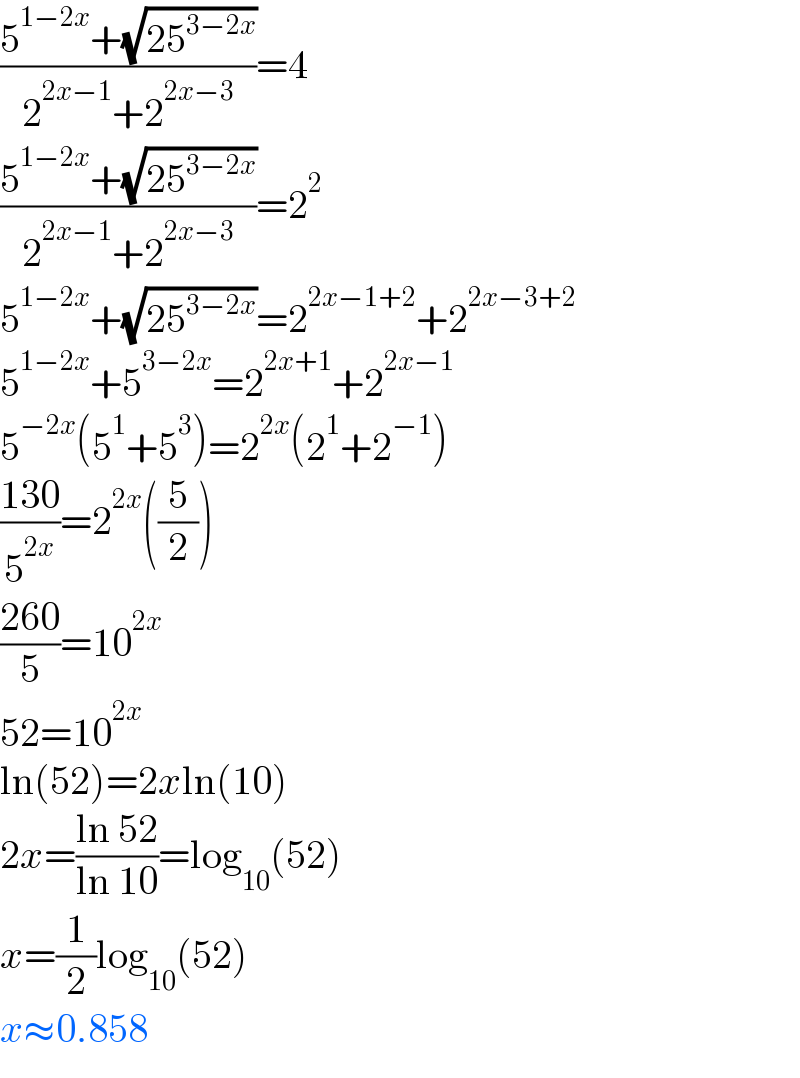
((5^(1−2x) +(√(25^(3−2x) )))/(2^(2x−1) +2^(2x−3) ))=4 ((5^(1−2x) +(√(25^(3−2x) )))/(2^(2x−1) +2^(2x−3) ))=2^2 5^(1−2x) +(√(25^(3−2x) ))=2^(2x−1+2) +2^(2x−3+2) 5^(1−2x) +5^(3−2x) =2^(2x+1) +2^(2x−1) 5^(−2x) (5^1 +5^3 )=2^(2x) (2^1 +2^(−1) ) ((130)/5^(2x) )=2^(2x) ((5/2)) ((260)/5)=10^(2x) 52=10^(2x) ln(52)=2xln(10) 2x=((ln 52)/(ln 10))=log_(10) (52) x=(1/2)log_(10) (52) x≈0.858

$$\frac{\mathrm{5}^{\mathrm{1}−\mathrm{2}{x}} +\sqrt{\mathrm{25}^{\mathrm{3}−\mathrm{2}{x}} }}{\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} +\mathrm{2}^{\mathrm{2}{x}−\mathrm{3}} }=\mathrm{4} \\ $$$$\frac{\mathrm{5}^{\mathrm{1}−\mathrm{2}{x}} +\sqrt{\mathrm{25}^{\mathrm{3}−\mathrm{2}{x}} }}{\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} +\mathrm{2}^{\mathrm{2}{x}−\mathrm{3}} }=\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{5}^{\mathrm{1}−\mathrm{2}{x}} +\sqrt{\mathrm{25}^{\mathrm{3}−\mathrm{2}{x}} }=\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}+\mathrm{2}} +\mathrm{2}^{\mathrm{2}{x}−\mathrm{3}+\mathrm{2}} \\ $$$$\mathrm{5}^{\mathrm{1}−\mathrm{2}{x}} +\mathrm{5}^{\mathrm{3}−\mathrm{2}{x}} =\mathrm{2}^{\mathrm{2}{x}+\mathrm{1}} +\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} \\ $$$$\mathrm{5}^{−\mathrm{2}{x}} \left(\mathrm{5}^{\mathrm{1}} +\mathrm{5}^{\mathrm{3}} \right)=\mathrm{2}^{\mathrm{2}{x}} \left(\mathrm{2}^{\mathrm{1}} +\mathrm{2}^{−\mathrm{1}} \right) \\ $$$$\frac{\mathrm{130}}{\mathrm{5}^{\mathrm{2}{x}} }=\mathrm{2}^{\mathrm{2}{x}} \left(\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{260}}{\mathrm{5}}=\mathrm{10}^{\mathrm{2}{x}} \\ $$$$\mathrm{52}=\mathrm{10}^{\mathrm{2}{x}} \\ $$$$\mathrm{ln}\left(\mathrm{52}\right)=\mathrm{2}{x}\mathrm{ln}\left(\mathrm{10}\right) \\ $$$$\mathrm{2}{x}=\frac{\mathrm{ln}\:\mathrm{52}}{\mathrm{ln}\:\mathrm{10}}=\mathrm{log}_{\mathrm{10}} \left(\mathrm{52}\right) \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}_{\mathrm{10}} \left(\mathrm{52}\right) \\ $$$${x}\approx\mathrm{0}.\mathrm{858} \\ $$

Answered by qaz last updated on 18/Nov/21

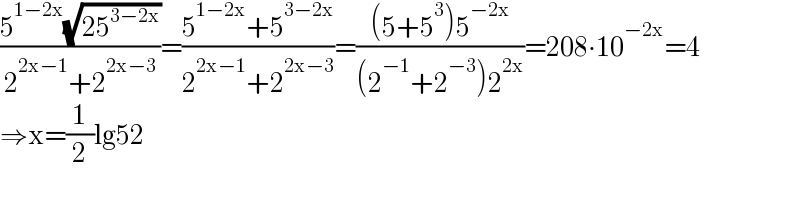
((5^(1−2x) (√(25^(3−2x) )))/(2^(2x−1) +2^(2x−3) ))=((5^(1−2x) +5^(3−2x) )/(2^(2x−1) +2^(2x−3) ))=(((5+5^3 )5^(−2x) )/((2^(−1) +2^(−3) )2^(2x) ))=208∙10^(−2x) =4 ⇒x=(1/2)lg52

$$\frac{\mathrm{5}^{\mathrm{1}−\mathrm{2x}} \sqrt{\mathrm{25}^{\mathrm{3}−\mathrm{2x}} }}{\mathrm{2}^{\mathrm{2x}−\mathrm{1}} +\mathrm{2}^{\mathrm{2x}−\mathrm{3}} }=\frac{\mathrm{5}^{\mathrm{1}−\mathrm{2x}} +\mathrm{5}^{\mathrm{3}−\mathrm{2x}} }{\mathrm{2}^{\mathrm{2x}−\mathrm{1}} +\mathrm{2}^{\mathrm{2x}−\mathrm{3}} }=\frac{\left(\mathrm{5}+\mathrm{5}^{\mathrm{3}} \right)\mathrm{5}^{−\mathrm{2x}} }{\left(\mathrm{2}^{−\mathrm{1}} +\mathrm{2}^{−\mathrm{3}} \right)\mathrm{2}^{\mathrm{2x}} }=\mathrm{208}\centerdot\mathrm{10}^{−\mathrm{2x}} =\mathrm{4} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lg52} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com