
Question Number 159327 by SANOGO last updated on 15/Nov/21

Answered by Derrick last updated on 16/Nov/21
![1)montrons que f est lineaire soient X=(x.y.z) et Y=(x′.y′.z′) on a: f(X+Y)=[(x+x′)+2(y+y′)+3(z+z′);2(x+x′)+(y+y′)+3(z+z′);−(x+x′)−(y+y′)−(z+z′)] =[x+2y+3z;2x+y+3z;−x−y−z]+[x′+2y′+3z′;2x′+y′+3z′;−x′−y′−z′] =f(X)+f(Y) ainsi f est lineaire](Q159366.png)
$$\left.\mathrm{1}\right){montrons}\:{que}\:{f}\:{est}\:{lineaire} \\ $$$${soient}\:{X}=\left({x}.{y}.{z}\right)\:{et}\:{Y}=\left({x}'.{y}'.{z}'\right) \\ $$$${on}\:{a}: \\ $$$${f}\left({X}+{Y}\right)=\left[\left({x}+{x}'\right)+\mathrm{2}\left({y}+{y}'\right)+\mathrm{3}\left({z}+{z}'\right);\mathrm{2}\left({x}+{x}'\right)+\left({y}+{y}'\right)+\mathrm{3}\left({z}+{z}'\right);−\left({x}+{x}'\right)−\left({y}+{y}'\right)−\left({z}+{z}'\right)\right] \\ $$$$=\left[{x}+\mathrm{2}{y}+\mathrm{3}{z};\mathrm{2}{x}+{y}+\mathrm{3}{z};−{x}−{y}−{z}\right]+\left[{x}'+\mathrm{2}{y}'+\mathrm{3}{z}';\mathrm{2}{x}'+{y}'+\mathrm{3}{z}';−{x}'−{y}'−{z}'\right] \\ $$$$={f}\left({X}\right)+{f}\left({Y}\right) \\ $$$${ainsi}\:{f}\:{est}\:{lineaire} \\ $$$$ \\ $$$$ \\ $$
Answered by Derrick last updated on 16/Nov/21
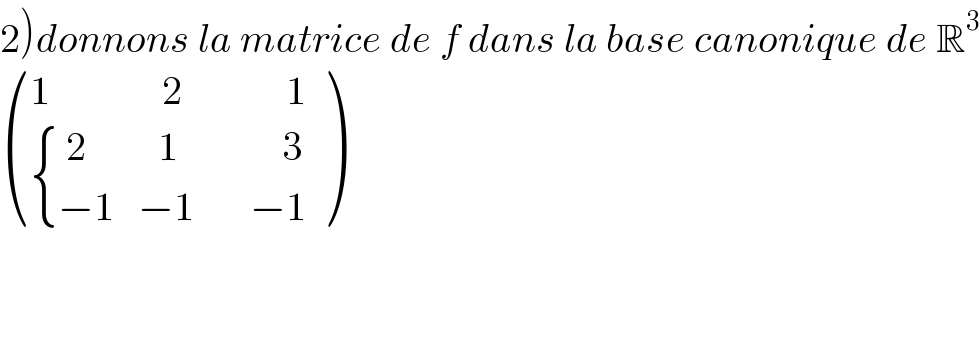
$$\left.\mathrm{2}\right){donnons}\:{la}\:{matrice}\:{de}\:{f}\:{dans}\:{la}\:{base}\:{canonique}\:{de}\:\mathbb{R}^{\mathrm{3}} \\ $$$$\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\begin{cases}{\:\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}}\\{−\mathrm{1}\:\:\:−\mathrm{1}\:\:\:\:\:\:\:−\mathrm{1}\:}\end{cases}}\end{pmatrix} \\ $$$$ \\ $$$$ \\ $$
Commented by SANOGO last updated on 16/Nov/21
$${merci}\:{bien} \\ $$
Answered by Derrick last updated on 16/Nov/21

$$\left.\mathrm{3}\left.\right){a}\right){determinons}\:{la}\:{dimension}\:{et}\:{une}\:{base}\:{de}\:{kerf} \\ $$$${soit}\:{X}=\left({x}.{y}.{z}\right)\in\mathbb{R}^{\mathrm{3}} \\ $$$${X}\in{kerf}\Leftrightarrow{AX}=\mathrm{0} \\ $$$$\Leftrightarrow{l}_{\mathrm{1}} \bullet{x}+\mathrm{2}{y}+{z}=\mathrm{0} \\ $$$$\:\:\:\:\:{l}_{\mathrm{2}} \bullet\mathrm{2}{x}+{y}+\mathrm{3}{z}=\mathrm{0} \\ $$$$\:\:\:{l}_{\mathrm{3}} \:\bullet−{x}−{y}−{z}=\mathrm{0} \\ $$$$\:{l}_{\mathrm{3}} \:\Rightarrow{x}=−{y}−{z} \\ $$$${l}_{\mathrm{3}} \:{dans}\:{l}_{\mathrm{2}} \:\Rightarrow{y}={z} \\ $$$${l}_{\mathrm{2}\:} {et}\:{l}_{\mathrm{3}} \:{dans}\:{l}_{\mathrm{1}} \:\Rightarrow{x}=−\mathrm{3}{z} \\ $$$${d}'{ou}:{X}=\left({x}.{y}.{z}\right)=\left(−\mathrm{3}{z},{z},{z}\right)={z}\left(−\mathrm{3},\mathrm{1},\mathrm{1}\right);{z}\in\mathbb{R} \\ $$$${kerf}=<\left(−\mathrm{3},\mathrm{1},\mathrm{1}\right)>={base}\:{de}\:{kerf} \\ $$$${on}\:{deduit}\:{donc}\:{que}\:: \\ $$$${dim}\left({kerf}\right)=\mathrm{1} \\ $$
Answered by Derrick last updated on 16/Nov/21

$$\left.{b}\right){puis}\:{dim}\left({kerf}\right)=\mathrm{1}≢\mathrm{0}\:{alors}\:{f}\:{n}'{est}\:{pas}\:{injective} \\ $$$$\left.\mathrm{4}\left.\right){a}\right){donnons}\:{le}\:{rang}\:{de}\:{f}\:{et}\:{une}\:{base}\:{de}\:{imf} \\ $$$${d}'{apres}\:{le}\:{theoreme}\:{du}\:{rang}\:{on}\:{a}: \\ $$$${dim}\left({kerf}\right)+{rang}\left({f}\right)=\mathrm{3} \\ $$$$\Rightarrow{rang}\left({f}\right)=\mathrm{3}−{dim}\left({kerf}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2} \\ $$$$\ast{donnons}\:{une}\:{base}\:{du}\:{imf} \\ $$$${V}=\left(\mathrm{1},\mathrm{2},\mathrm{1}\right)\:{et}\:{U}=\left(−\mathrm{1},−\mathrm{1},−\mathrm{1}\right)\:{sont}\:{dans}\:{imf}\:{et}\:{de}\:{plus}\:{il}\:{forme}\:{un}\:{systeme}\:{libre}\: \\ $$$${donc}\:{une}\:{base}\:{du}\:{imf}\:{est}: \\ $$$${B}=<{V},{U}> \\ $$$$\left.{b}\right){remarqu}'{on}\:{que}\:{la}\:{dimension}\:{de}\:{l}'{espace}\:{de}\:{depart}\:{et}\:{d}'{arrivee}\:{est}\:\mathrm{3}\: \\ $$$${ainsi}\:{donc}: \\ $$$${f}\:{injecrive}\Leftrightarrow{f}\:{surjective}\Leftrightarrow{f}\:{bijecrive} \\ $$$${puisque}\:{f}\:{n}'{est}\:{pas}\:{innective}\:{alors}\:{on}\:{en}\:{deduit}\:{que}\:{f}\:{n}'{est}\:{pas}\:{surjective} \\ $$$$\ldots{derrick}\ldots \\ $$
Commented by SANOGO last updated on 16/Nov/21
$${merci}\:{bien} \\ $$
