Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 159005 by Tawa11 last updated on 11/Nov/21

Answered by ajfour last updated on 12/Nov/21

s=2rsin α p=rsin 2α cos β=((35/2)/r) =(7/8); sin β=((√(15))/8) ((sin (90°−α))/(27))=((sin (3α+β))/p) 20sin 2αcos α=27sin (3α+β) 10sin α+37sin 3α=27sin (3α+β)+27sin 3α =27cos β{3sin α−4sin^3 α +((√(15))/7)(4cos^3 α−3cos α)} say tan α=m 40=27×(7/8){3(1+m^2 )−4m^3 +((√(15))/7)[4−3(1+m^2 )]} ...we need a straight cubic formula...still trying!

$${s}=\mathrm{2}{r}\mathrm{sin}\:\alpha \\ $$$${p}={r}\mathrm{sin}\:\mathrm{2}\alpha \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{35}/\mathrm{2}}{{r}}\:=\frac{\mathrm{7}}{\mathrm{8}};\:\:\mathrm{sin}\:\beta=\frac{\sqrt{\mathrm{15}}}{\mathrm{8}} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{90}°−\alpha\right)}{\mathrm{27}}=\frac{\mathrm{sin}\:\left(\mathrm{3}\alpha+\beta\right)}{{p}} \\ $$$$\mathrm{20sin}\:\mathrm{2}\alpha\mathrm{cos}\:\alpha=\mathrm{27sin}\:\left(\mathrm{3}\alpha+\beta\right) \\ $$$$\mathrm{10sin}\:\alpha+\mathrm{37sin}\:\mathrm{3}\alpha=\mathrm{27sin}\:\left(\mathrm{3}\alpha+\beta\right)+\mathrm{27sin}\:\mathrm{3}\alpha \\ $$$$\:\:\:=\mathrm{27cos}\:\beta\left\{\mathrm{3sin}\:\alpha−\mathrm{4sin}\:^{\mathrm{3}} \alpha\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\sqrt{\mathrm{15}}}{\mathrm{7}}\left(\mathrm{4cos}\:^{\mathrm{3}} \alpha−\mathrm{3cos}\:\alpha\right)\right\} \\ $$$${say}\:\:\mathrm{tan}\:\alpha={m} \\ $$$$\mathrm{40}=\mathrm{27}×\frac{\mathrm{7}}{\mathrm{8}}\left\{\mathrm{3}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)−\mathrm{4}{m}^{\mathrm{3}} \right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\sqrt{\mathrm{15}}}{\mathrm{7}}\left[\mathrm{4}−\mathrm{3}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\right]\right\} \\ $$$$...{we}\:{need}\:{a}\:{straight}\:{cubic}\: \\ $$$${formula}...{still}\:{trying}! \\ $$

Commented by Tawa11 last updated on 12/Nov/21

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by mr W last updated on 11/Nov/21

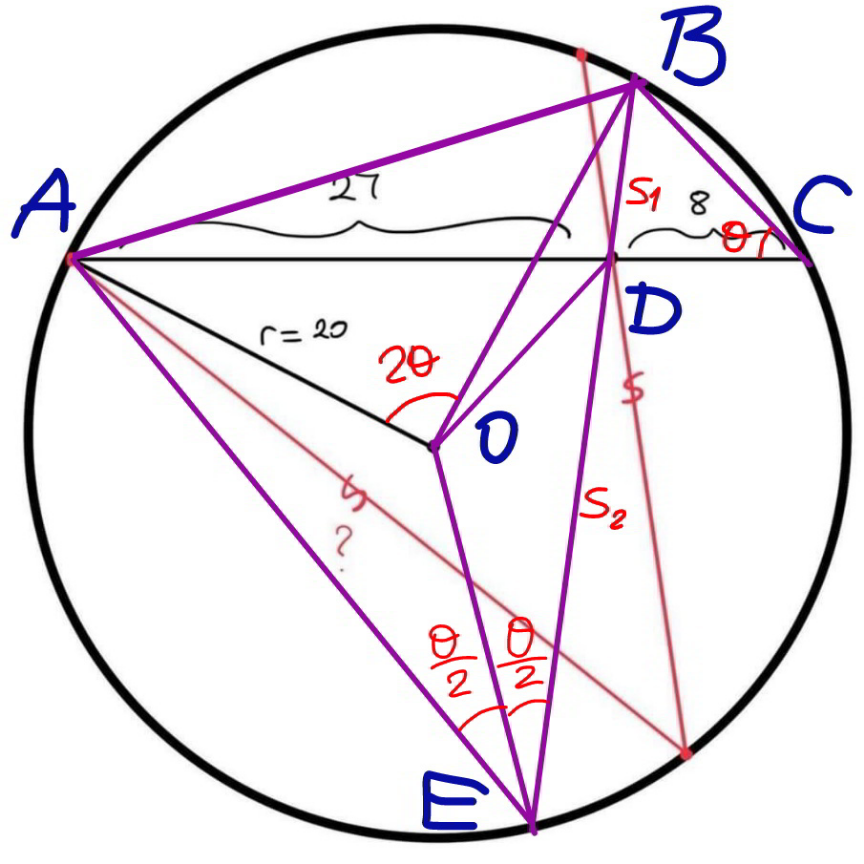
Commented by mr W last updated on 12/Nov/21

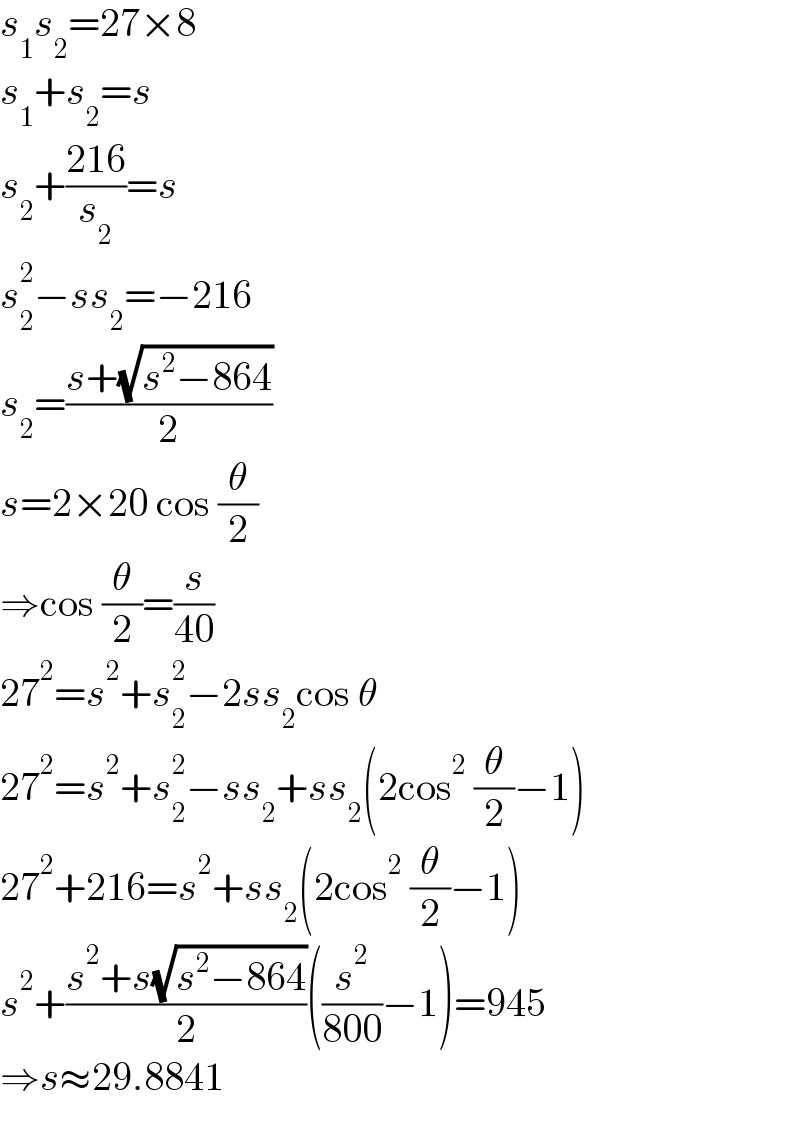
s_1 s_2 =27×8 s_1 +s_2 =s s_2 +((216)/s_2 )=s s_2 ^2 −ss_2 =−216 s_2 =((s+(√(s^2 −864)))/2) s=2×20 cos (θ/2) ⇒cos (θ/2)=(s/(40)) 27^2 =s^2 +s_2 ^2 −2ss_2 cos θ 27^2 =s^2 +s_2 ^2 −ss_2 +ss_2 (2cos^2 (θ/2)−1) 27^2 +216=s^2 +ss_2 (2cos^2 (θ/2)−1) s^2 +((s^2 +s(√(s^2 −864)))/2)((s^2 /(800))−1)=945 ⇒s≈29.8841

$${s}_{\mathrm{1}} {s}_{\mathrm{2}} =\mathrm{27}×\mathrm{8} \\ $$$${s}_{\mathrm{1}} +{s}_{\mathrm{2}} ={s} \\ $$$${s}_{\mathrm{2}} +\frac{\mathrm{216}}{{s}_{\mathrm{2}} }={s} \\ $$$${s}_{\mathrm{2}} ^{\mathrm{2}} −{ss}_{\mathrm{2}} =−\mathrm{216} \\ $$$${s}_{\mathrm{2}} =\frac{{s}+\sqrt{{s}^{\mathrm{2}} −\mathrm{864}}}{\mathrm{2}} \\ $$$${s}=\mathrm{2}×\mathrm{20}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\frac{{s}}{\mathrm{40}} \\ $$$$\mathrm{27}^{\mathrm{2}} ={s}^{\mathrm{2}} +{s}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2}{ss}_{\mathrm{2}} \mathrm{cos}\:\theta \\ $$$$\mathrm{27}^{\mathrm{2}} ={s}^{\mathrm{2}} +{s}_{\mathrm{2}} ^{\mathrm{2}} −{ss}_{\mathrm{2}} +{ss}_{\mathrm{2}} \left(\mathrm{2cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\mathrm{27}^{\mathrm{2}} +\mathrm{216}={s}^{\mathrm{2}} +{ss}_{\mathrm{2}} \left(\mathrm{2cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}−\mathrm{1}\right) \\ $$$${s}^{\mathrm{2}} +\frac{{s}^{\mathrm{2}} +{s}\sqrt{{s}^{\mathrm{2}} −\mathrm{864}}}{\mathrm{2}}\left(\frac{{s}^{\mathrm{2}} }{\mathrm{800}}−\mathrm{1}\right)=\mathrm{945} \\ $$$$\Rightarrow{s}\approx\mathrm{29}.\mathrm{8841} \\ $$

Commented by Tawa11 last updated on 12/Nov/21

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com