
Question Number 158924 by ajfour last updated on 10/Nov/21
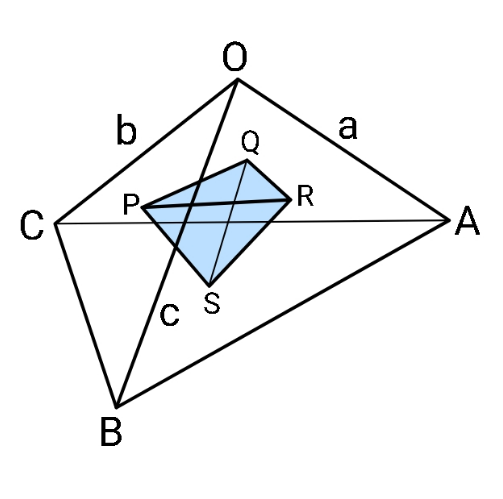
Commented by ajfour last updated on 10/Nov/21

$${a},\:{b},\:{c}\:{are}\:{slant}\:{edges}\:{of}\:{outer} \\ $$$${tetrahedron}.\:{Find}\:{minimum} \\ $$$${volume}\:{of}\:{inner}\:{tetrahedron} \\ $$$${whose}\:{vertices}\:{lie}\:{on}\:{faces}\:{of} \\ $$$${outer}\:{one}\:{when}\:{the}\:{outer}\:{one} \\ $$$$\:\:\:\:{has}\:{a}\:{maximum}\:{volume}. \\ $$
Commented by ajfour last updated on 10/Nov/21

$${thanks},{Sir};\:{i}\:{did}\:{blunder}! \\ $$
Commented by mr W last updated on 10/Nov/21
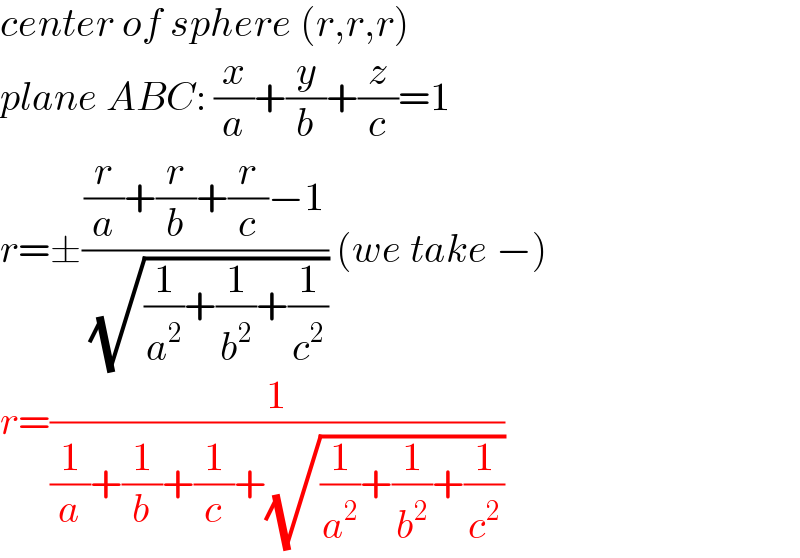
$${center}\:{of}\:{sphere}\:\left({r},{r},{r}\right)\: \\ $$$${plane}\:{ABC}:\:\frac{{x}}{{a}}+\frac{{y}}{{b}}+\frac{{z}}{{c}}=\mathrm{1} \\ $$$${r}=\pm\frac{\frac{{r}}{{a}}+\frac{{r}}{{b}}+\frac{{r}}{{c}}−\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}}\:\left({we}\:{take}\:−\right) \\ $$$${r}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}} \\ $$
Answered by mr W last updated on 10/Nov/21

$${Part}\:{I} \\ $$$${say}\:\theta={angle}\:{between}\:{OA}\:{and}\:{OB} \\ $$$${say}\:\varphi={angle}\:{betw}.\:{OC}\:{and}\:{plane}\:{OAB} \\ $$$${then}\:{the}\:{volume}\:{of}\:{the}\:{outer} \\ $$$${tetrahedron}\:{is} \\ $$$${V}_{{O}} =\frac{\mathrm{1}}{\mathrm{3}}×\frac{{ab}\:\mathrm{sin}\:\theta}{\mathrm{2}}×{c}\:\mathrm{sin}\:\varphi=\frac{{abc}\:\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi}{\mathrm{6}} \\ $$$${it}'{s}\:{clear}\:{V}_{{O}} \:{is}\:{maximum}\:{when} \\ $$$$\theta=\varphi=\mathrm{90}°,\:{i}.{e}.\:{a},{b},{c}\:{are}\:{perpendicular} \\ $$$${to}\:{each}\:{other}. \\ $$
