
Question Number 158893 by ajfour last updated on 10/Nov/21
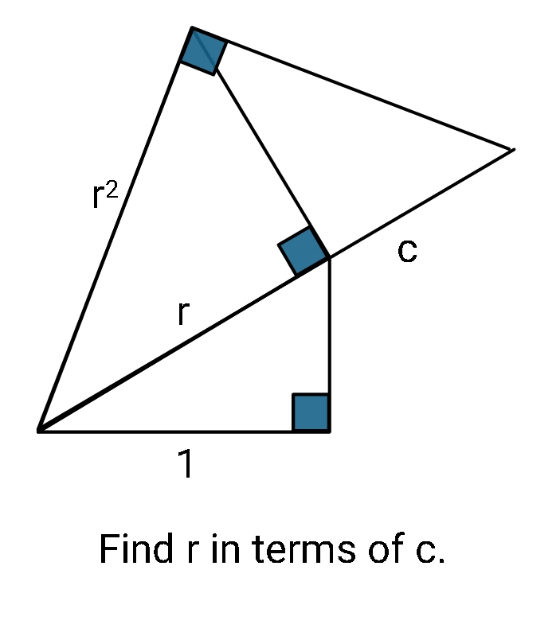
Answered by ajfour last updated on 10/Nov/21
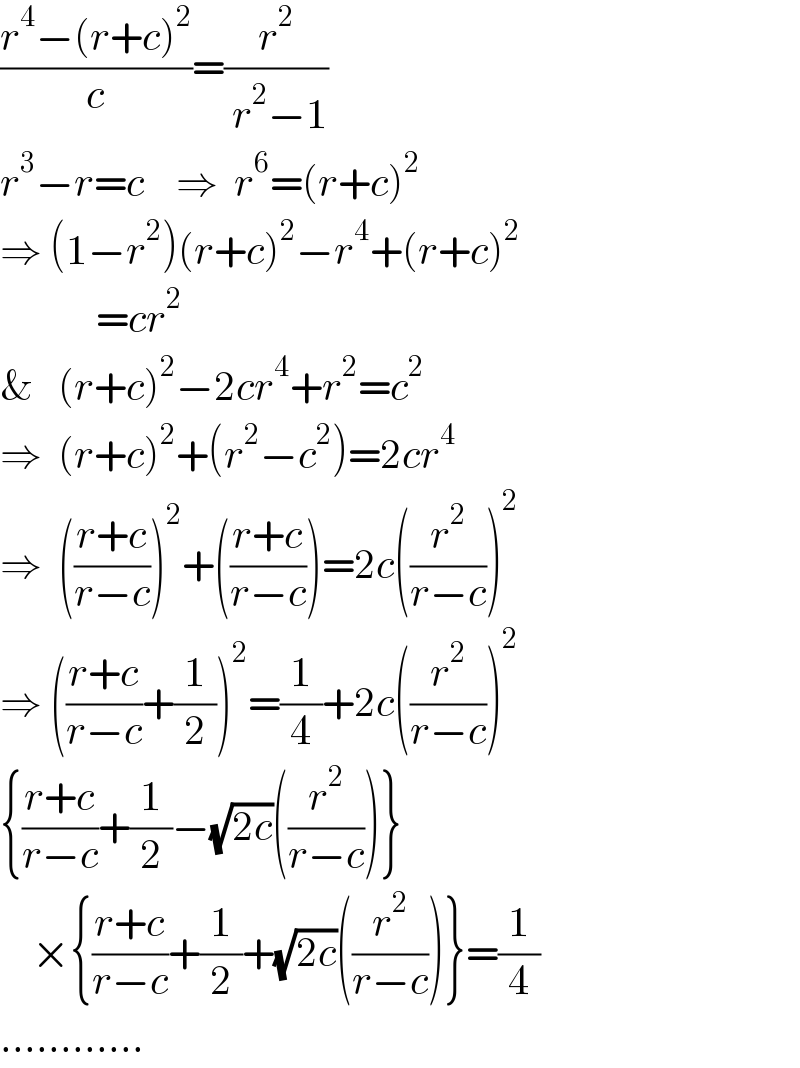
$$\frac{{r}^{\mathrm{4}} −\left({r}+{c}\right)^{\mathrm{2}} }{{c}}=\frac{{r}^{\mathrm{2}} }{\:{r}^{\mathrm{2}} −\mathrm{1}} \\ $$$${r}^{\mathrm{3}} −{r}={c}\:\:\:\:\Rightarrow\:\:{r}^{\mathrm{6}} =\left({r}+{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{1}−{r}^{\mathrm{2}} \right)\left({r}+{c}\right)^{\mathrm{2}} −{r}^{\mathrm{4}} +\left({r}+{c}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={cr}^{\mathrm{2}} \\ $$$$\&\:\:\:\left({r}+{c}\right)^{\mathrm{2}} −\mathrm{2}{cr}^{\mathrm{4}} +{r}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left({r}+{c}\right)^{\mathrm{2}} +\left({r}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)=\mathrm{2}{cr}^{\mathrm{4}} \\ $$$$\Rightarrow\:\:\left(\frac{{r}+{c}}{{r}−{c}}\right)^{\mathrm{2}} +\left(\frac{{r}+{c}}{{r}−{c}}\right)=\mathrm{2}{c}\left(\frac{{r}^{\mathrm{2}} }{{r}−{c}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\frac{{r}+{c}}{{r}−{c}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}{c}\left(\frac{{r}^{\mathrm{2}} }{{r}−{c}}\right)^{\mathrm{2}} \\ $$$$\left\{\frac{{r}+{c}}{{r}−{c}}+\frac{\mathrm{1}}{\mathrm{2}}−\sqrt{\mathrm{2}{c}}\left(\frac{{r}^{\mathrm{2}} }{{r}−{c}}\right)\right\} \\ $$$$\:\:\:\:×\left\{\frac{{r}+{c}}{{r}−{c}}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{2}{c}}\left(\frac{{r}^{\mathrm{2}} }{{r}−{c}}\right)\right\}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$............ \\ $$
