Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 158281 by Ari last updated on 01/Nov/21

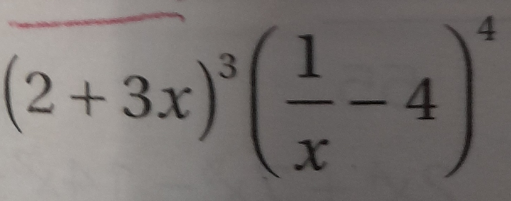
Commented by Ari last updated on 01/Nov/21

Find the constant term on the decomposition of expression

Commented by cortano last updated on 02/Nov/21

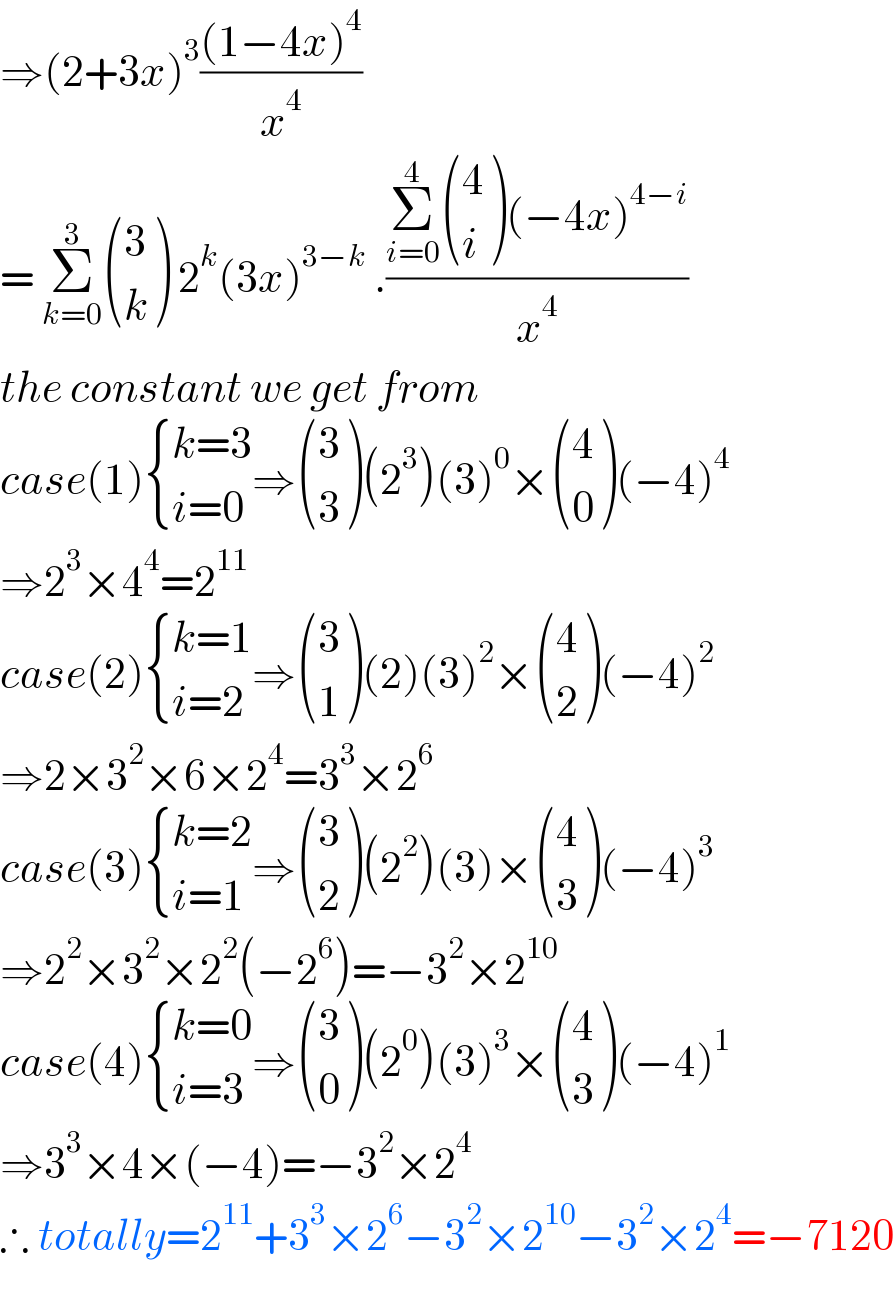
⇒(2+3x)^3 (((1−4x)^4 )/x^4 ) = Σ_(k=0) ^3 ((3),(k) ) 2^k (3x)^(3−k) .((Σ_(i=0) ^4 ((4),(i) )(−4x)^(4−i) )/x^4 ) the constant we get from case(1) { ((k=3)),((i=0)) :}⇒ ((3),(3) )(2^3 )(3)^0 × ((4),(0) )(−4)^4 ⇒2^3 ×4^4 =2^(11) case(2) { ((k=1)),((i=2)) :}⇒ ((3),(1) )(2)(3)^2 × ((4),(2) )(−4)^2 ⇒2×3^2 ×6×2^4 =3^3 ×2^6 case(3) { ((k=2)),((i=1)) :}⇒ ((3),(2) )(2^2 )(3)× ((4),(3) )(−4)^3 ⇒2^2 ×3^2 ×2^2 (−2^6 )=−3^2 ×2^(10) case(4) { ((k=0)),((i=3)) :}⇒ ((3),(0) )(2^0 )(3)^3 × ((4),(3) )(−4)^1 ⇒3^3 ×4×(−4)=−3^2 ×2^4 ∴ totally=2^(11) +3^3 ×2^6 −3^2 ×2^(10) −3^2 ×2^4 =−7120

$$\Rightarrow\left(\mathrm{2}+\mathrm{3}{x}\right)^{\mathrm{3}} \frac{\left(\mathrm{1}−\mathrm{4}{x}\right)^{\mathrm{4}} }{{x}^{\mathrm{4}} } \\ $$$$=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\begin{pmatrix}{\mathrm{3}}\\{{k}}\end{pmatrix}\:\mathrm{2}^{{k}} \left(\mathrm{3}{x}\right)^{\mathrm{3}−{k}} \:.\frac{\underset{{i}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}\begin{pmatrix}{\mathrm{4}}\\{{i}}\end{pmatrix}\left(−\mathrm{4}{x}\right)^{\mathrm{4}−{i}} }{{x}^{\mathrm{4}} } \\ $$$${the}\:{constant}\:{we}\:{get}\:{from} \\ $$$${case}\left(\mathrm{1}\right)\begin{cases}{{k}=\mathrm{3}}\\{{i}=\mathrm{0}}\end{cases}\Rightarrow\begin{pmatrix}{\mathrm{3}}\\{\mathrm{3}}\end{pmatrix}\left(\mathrm{2}^{\mathrm{3}} \right)\left(\mathrm{3}\right)^{\mathrm{0}} ×\begin{pmatrix}{\mathrm{4}}\\{\mathrm{0}}\end{pmatrix}\left(−\mathrm{4}\right)^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{3}} ×\mathrm{4}^{\mathrm{4}} =\mathrm{2}^{\mathrm{11}} \\ $$$${case}\left(\mathrm{2}\right)\begin{cases}{{k}=\mathrm{1}}\\{{i}=\mathrm{2}}\end{cases}\Rightarrow\begin{pmatrix}{\mathrm{3}}\\{\mathrm{1}}\end{pmatrix}\left(\mathrm{2}\right)\left(\mathrm{3}\right)^{\mathrm{2}} ×\begin{pmatrix}{\mathrm{4}}\\{\mathrm{2}}\end{pmatrix}\left(−\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}×\mathrm{3}^{\mathrm{2}} ×\mathrm{6}×\mathrm{2}^{\mathrm{4}} =\mathrm{3}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{6}} \\ $$$${case}\left(\mathrm{3}\right)\begin{cases}{{k}=\mathrm{2}}\\{{i}=\mathrm{1}}\end{cases}\Rightarrow\begin{pmatrix}{\mathrm{3}}\\{\mathrm{2}}\end{pmatrix}\left(\mathrm{2}^{\mathrm{2}} \right)\left(\mathrm{3}\right)×\begin{pmatrix}{\mathrm{4}}\\{\mathrm{3}}\end{pmatrix}\left(−\mathrm{4}\right)^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} \left(−\mathrm{2}^{\mathrm{6}} \right)=−\mathrm{3}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{10}} \\ $$$${case}\left(\mathrm{4}\right)\begin{cases}{{k}=\mathrm{0}}\\{{i}=\mathrm{3}}\end{cases}\Rightarrow\begin{pmatrix}{\mathrm{3}}\\{\mathrm{0}}\end{pmatrix}\left(\mathrm{2}^{\mathrm{0}} \right)\left(\mathrm{3}\right)^{\mathrm{3}} ×\begin{pmatrix}{\mathrm{4}}\\{\mathrm{3}}\end{pmatrix}\left(−\mathrm{4}\right)^{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{3}} ×\mathrm{4}×\left(−\mathrm{4}\right)=−\mathrm{3}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{4}} \\ $$$$\therefore\:{totally}=\mathrm{2}^{\mathrm{11}} +\mathrm{3}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{6}} −\mathrm{3}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{10}} −\mathrm{3}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{4}} =−\mathrm{7120} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com