Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 158035 by HongKing last updated on 30/Oct/21

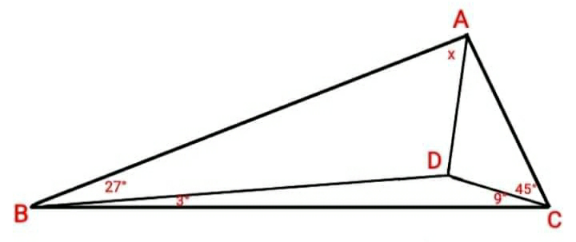
Answered by mr W last updated on 30/Oct/21

say BC=1 ((BD)/(sin 9))=(1/(sin (3+9))) ⇒BD=((sin 9)/(sin 12)) ((BA)/(sin (9+45)))=(1/(sin (27+3+9+45))) ⇒BA=((sin 54)/(sin 84)) ((sin (x+27))/(sin x))=((BA)/(BD))=((sin 54)/(sin 84))×((sin 12)/(sin 9)) cos 27+((sin 27)/(tan x))=((sin 54)/(sin 84))×((sin 12)/(sin 9)) tan x=((sin 27)/(((sin 54)/(sin 84))×((sin 12)/(sin 9))−cos 27)) x=tan^(−1) (((sin 27)/(((sin 54)/(sin 84))×((sin 12)/(sin 9))−cos 27)))≈67.3°

$${say}\:{BC}=\mathrm{1} \\ $$$$\frac{{BD}}{\mathrm{sin}\:\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{sin}\:\left(\mathrm{3}+\mathrm{9}\right)}\: \\ $$$$\Rightarrow{BD}=\frac{\mathrm{sin}\:\mathrm{9}}{\mathrm{sin}\:\mathrm{12}} \\ $$$$\frac{{BA}}{\mathrm{sin}\:\left(\mathrm{9}+\mathrm{45}\right)}=\frac{\mathrm{1}}{\mathrm{sin}\:\left(\mathrm{27}+\mathrm{3}+\mathrm{9}+\mathrm{45}\right)} \\ $$$$\Rightarrow{BA}=\frac{\mathrm{sin}\:\mathrm{54}}{\mathrm{sin}\:\mathrm{84}} \\ $$$$\frac{\mathrm{sin}\:\left({x}+\mathrm{27}\right)}{\mathrm{sin}\:{x}}=\frac{{BA}}{{BD}}=\frac{\mathrm{sin}\:\mathrm{54}}{\mathrm{sin}\:\mathrm{84}}×\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{9}} \\ $$$$\mathrm{cos}\:\mathrm{27}+\frac{\mathrm{sin}\:\mathrm{27}}{\mathrm{tan}\:{x}}=\frac{\mathrm{sin}\:\mathrm{54}}{\mathrm{sin}\:\mathrm{84}}×\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{9}} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{sin}\:\mathrm{27}}{\frac{\mathrm{sin}\:\mathrm{54}}{\mathrm{sin}\:\mathrm{84}}×\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{9}}−\mathrm{cos}\:\mathrm{27}} \\ $$$${x}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{27}}{\frac{\mathrm{sin}\:\mathrm{54}}{\mathrm{sin}\:\mathrm{84}}×\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{9}}−\mathrm{cos}\:\mathrm{27}}\right)\approx\mathrm{67}.\mathrm{3}° \\ $$

Commented by HongKing last updated on 31/Oct/21

cool my dear See thank you so much

$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{ee}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com