
Question Number 156511 by KONE last updated on 12/Oct/21

Answered by KONE last updated on 12/Oct/21
$${svp}\:{aide}\:{dans}\:{la}\:{question}\:\mathrm{2} \\ $$
Answered by mindispower last updated on 12/Oct/21
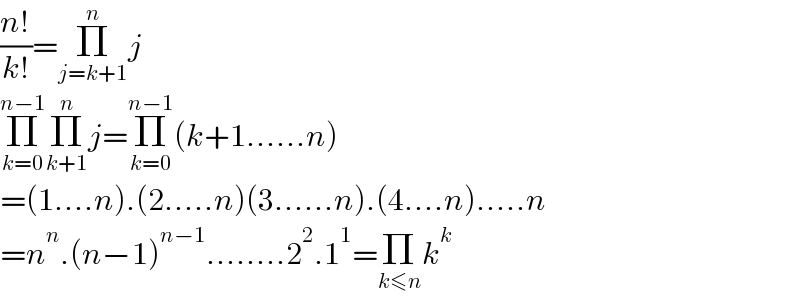
$$\frac{{n}!}{{k}!}=\underset{{j}={k}+\mathrm{1}} {\overset{{n}} {\prod}}{j} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\underset{{k}+\mathrm{1}} {\overset{{n}} {\prod}}{j}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\mathrm{1}......{n}\right) \\ $$$$=\left(\mathrm{1}....{n}\right).\left(\mathrm{2}.....{n}\right)\left(\mathrm{3}......{n}\right).\left(\mathrm{4}....{n}\right).....{n} \\ $$$$={n}^{{n}} .\left({n}−\mathrm{1}\right)^{{n}−\mathrm{1}} ........\mathrm{2}^{\mathrm{2}} .\mathrm{1}^{\mathrm{1}} =\underset{{k}\leqslant{n}} {\prod}{k}^{{k}} \\ $$
Commented by puissant last updated on 12/Oct/21

$${Good}\:{sir}\:{Mindispower}... \\ $$$${Mr}\:{Kone}\:{c}'{est}\:{bien}\:{de}\:{dire}\:{merci}\:{pour} \\ $$$${montrer}\:{a}\:{celui}\:{qui}\:{t}'{a}\:{aid}\acute {{e}}\:{que}\:{tu}\:{as}\: \\ $$$${vu}\:{la}\:{reponse}\:{et}\:{que}\:{tu}\:{apprecies}... \\ $$$${ca}\:{ferra}\:{en}\:{sorte}\:{que}\:{prochainement} \\ $$$${on}\:{t}'{aide}\:{facilement}...\: \\ $$$${bonne}\:{continuation}... \\ $$
Commented by KONE last updated on 13/Oct/21

$${salut}\:{a}\:{vous}\:{je}\:{m}'{excuse}\:{ma}\:{connexion}\:{n}'{etais}\:{pas}\:{trop}\:{en}\:{place} \\ $$$${merci}\:{bien}\:{a}\:{vous}\:{pour}\:{votre}\:{assistance} \\ $$
Commented by KONE last updated on 13/Oct/21
$${svp}\:{je}\:{ne}\:{comprendsas}\:{trop}\:{la}\:{premiere}\:{ligne} \\ $$
Commented by puissant last updated on 14/Oct/21

$${Remarque}\:{que}\:{le}\:{produit}\:{commence}\:{a} \\ $$$${k}+\mathrm{1}\:{en}\:{fait}\:{ca}\:{va}\:{devenir}\: \\ $$$$\underset{{j}={k}+\mathrm{1}} {\overset{{n}} {\prod}}=\:\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)....{n}\:{or}\:{pour}\:{ecrire}\:{factoriel} \\ $$$${n},\:{il}\:{faut}\:{commencer}\:{a}\:\mathrm{1}\:{cet}\:{a}\:{dire} \\ $$$$\mathrm{1}.\mathrm{2}.\mathrm{3}....{n}\:{maintenant}\:{comme}\:{on}\:{a}\:{pas}\:{ca}, \\ $$$${on}\:{ajoute}\:\mathrm{1}.\mathrm{2}.\mathrm{3}...{k}={k}!\:{en}\:{haut}\:{et}\:{en}\: \\ $$$${bas}\:{cet}\:{a}\:{dire}\:{n}\left({n}−\mathrm{1}\right)....\left({k}+\mathrm{1}\right)\frac{{k}\left({k}−\mathrm{1}\right)...\mathrm{2}.\mathrm{1}}{{k}\left({k}−\mathrm{1}\right)...\mathrm{2}.\mathrm{1}} \\ $$$${ca}\:{devient}\:{alors}\:: \\ $$$$\:\frac{{n}\left({n}−\mathrm{1}\right)...\left({k}+\mathrm{1}\right){k}\left({k}−\mathrm{1}\right)....\mathrm{2}.\mathrm{1}}{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)....\mathrm{2}.\mathrm{1}}\:=\:\frac{{n}!}{{k}!} \\ $$$${bref}\:{c}'{est}\:{juste}\:{un}\:{petit}\:{jeu}\:{sur}\:{le}\:{produit} \\ $$$${qu}'{il}\:{faut}\:{remarquer}... \\ $$$$ \\ $$$${Cordialement}.. \\ $$
