
Question Number 15642 by mrW1 last updated on 12/Jun/17
Answered by ajfour last updated on 12/Jun/17
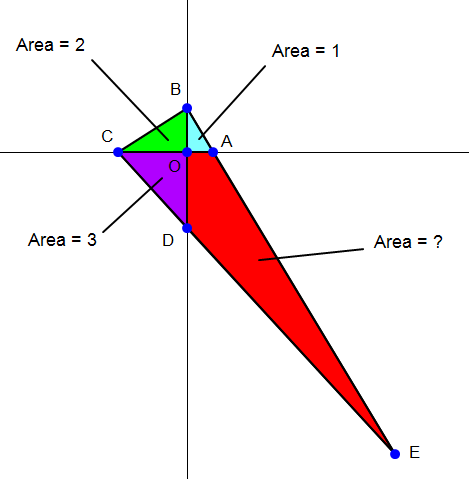
![Required Area=S let O be origin. A(a,0) ; B(0,b) ; C(−c,0) ; D(0,−d) ; E(a+p, −d−q) ((q+d)/p)=(b/a) , ((p+a)/q)=(c/d) ⇒ aq+ad=bp ...(i) dp+ad=cq ...(ii) or acq+adc=bpc and adp+a^2 d=acq adding: adc+adp+a^2 d=bpc p(bc−ad)=ad(c−a) p=((ad(c+a))/(bc−ad)) ...(iii) (i)−(ii) gives: aq−dp=bp−cq or q(a+c)=p(b+d) q=(((b+d)/(a+c)))p substituting for p=((ad(c+a))/(bc−ad)) ; q=((ad(b+d))/(bc−ad)) Now, S+((p(d+q))/2)+((q(a+p))/2) =(a+p)(d+q) ⇒ 2S+dp+pq+aq+pq =2ad+2aq+2dp+2pq or S= (1/2)(aq+dp+2ad) S= (1/2)[((a^2 d(b+d))/(bc−ad))+((ad^2 (c+a))/(bc−ad))+2ad] =((ad)/(2(bc−ad)))(ab+ad+cd+ad+2bc−2ad) S=((ad)/(2(bc−ad)))(ab+2bc+cd) (c/a)=((Area(ΔBOC))/(Area(ΔAOB))) = 2 (d/b)=((Area(ΔCOD))/(Area(ΔBOC))) =(3/2) ⇒ ((ad)/(bc))=(((a/c))/((b/d)))=(((1/2))/((2/3)))=(3/4) ad= (3/4)(bc) from areas ((ab)/2)=1 ⇒ ab=2 ((bc)/2)=2 ⇒ bc=4 ((cd)/2)=3 ⇒ cd=6 and as ad=(3/4)(bc) ⇒ ad=(3/4)×4=3 substituting for these in expression obtained for S, S=((ad)/(2(bc−ad)))(ab+2bc+cd) =(3/(2(4−3)))×(2+8+6) S=24 sq.units .](Q15649.png)
$$\:\:{Required}\:{Area}={S} \\ $$$$\:{let}\:{O}\:{be}\:{origin}. \\ $$$$\:{A}\left({a},\mathrm{0}\right)\:;\:{B}\left(\mathrm{0},{b}\right)\:;\:{C}\left(−{c},\mathrm{0}\right)\:; \\ $$$$\:{D}\left(\mathrm{0},−{d}\right)\:;\:{E}\left({a}+{p},\:−{d}−{q}\right) \\ $$$$\:\:\frac{{q}+{d}}{{p}}=\frac{{b}}{{a}}\:\:\:,\:\:\:\:\:\frac{{p}+{a}}{{q}}=\frac{{c}}{{d}} \\ $$$$\Rightarrow\:{aq}+{ad}={bp}\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\left({i}\right) \\ $$$$\:\:\:\:\:\:{dp}+{ad}={cq}\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\left({ii}\right) \\ $$$${or}\:\:\:\:\:\:{acq}+{adc}={bpc}\:\:{and} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{adp}+{a}^{\mathrm{2}} {d}={acq} \\ $$$${adding}:\:\:\:{adc}+{adp}+{a}^{\mathrm{2}} {d}={bpc} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{p}\left({bc}−{ad}\right)={ad}\left({c}−{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{p}=\frac{{ad}\left({c}+{a}\right)}{{bc}−{ad}}\:\:\:\:\:\:\:\:\:...\left({iii}\right) \\ $$$$\:\:\:\:\left({i}\right)−\left({ii}\right)\:{gives}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{aq}−{dp}={bp}−{cq} \\ $$$${or}\:\:\:\:\:\:\:\:\:{q}\left({a}+{c}\right)={p}\left({b}+{d}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{q}=\left(\frac{{b}+{d}}{{a}+{c}}\right){p} \\ $$$${substituting}\:{for}\: \\ $$$$\:\:\:\:\:\:\:\:{p}=\frac{{ad}\left({c}+{a}\right)}{{bc}−{ad}}\:;\:\:{q}=\frac{{ad}\left({b}+{d}\right)}{{bc}−{ad}} \\ $$$$\:{Now},\:\:\:{S}+\frac{{p}\left({d}+{q}\right)}{\mathrm{2}}+\frac{{q}\left({a}+{p}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}+{p}\right)\left({d}+{q}\right) \\ $$$$\Rightarrow\:\:\mathrm{2}{S}+{dp}+{pq}+{aq}+{pq} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{ad}+\mathrm{2}{aq}+\mathrm{2}{dp}+\mathrm{2}{pq} \\ $$$${or}\:\:{S}=\:\frac{\mathrm{1}}{\mathrm{2}}\left({aq}+{dp}+\mathrm{2}{ad}\right) \\ $$$${S}=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{a}^{\mathrm{2}} {d}\left({b}+{d}\right)}{{bc}−{ad}}+\frac{{ad}^{\mathrm{2}} \left({c}+{a}\right)}{{bc}−{ad}}+\mathrm{2}{ad}\right] \\ $$$$=\frac{{ad}}{\mathrm{2}\left({bc}−{ad}\right)}\left({ab}+{ad}+{cd}+{ad}+\mathrm{2}{bc}−\mathrm{2}{ad}\right) \\ $$$$\:\:\:{S}=\frac{{ad}}{\mathrm{2}\left({bc}−{ad}\right)}\left({ab}+\mathrm{2}{bc}+{cd}\right) \\ $$$$\:\:\:\:\:\frac{{c}}{{a}}=\frac{{Area}\left(\Delta{BOC}\right)}{{Area}\left(\Delta{AOB}\right)}\:=\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\frac{{d}}{{b}}=\frac{{Area}\left(\Delta{COD}\right)}{{Area}\left(\Delta{BOC}\right)}\:=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{{ad}}{{bc}}=\frac{\left({a}/{c}\right)}{\left({b}/{d}\right)}=\frac{\left(\mathrm{1}/\mathrm{2}\right)}{\left(\mathrm{2}/\mathrm{3}\right)}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{ad}=\:\frac{\mathrm{3}}{\mathrm{4}}\left({bc}\right) \\ $$$$\:{from}\:{areas}\:\:\:\:\frac{{ab}}{\mathrm{2}}=\mathrm{1}\:\:\Rightarrow\:\:{ab}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{bc}}{\mathrm{2}}=\mathrm{2}\:\:\:\Rightarrow\:\:{bc}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{cd}}{\mathrm{2}}=\mathrm{3}\:\:\:\Rightarrow\:\:{cd}=\mathrm{6} \\ $$$$\:\:\:{and}\:{as}\:\:{ad}=\frac{\mathrm{3}}{\mathrm{4}}\left({bc}\right)\:\:\Rightarrow\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ad}=\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{4}=\mathrm{3} \\ $$$${substituting}\:{for}\:{these}\:{in} \\ $$$${expression}\:{obtained}\:{for}\:{S},\: \\ $$$$\:\:\:{S}=\frac{{ad}}{\mathrm{2}\left({bc}−{ad}\right)}\left({ab}+\mathrm{2}{bc}+{cd}\right) \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{4}−\mathrm{3}\right)}×\left(\mathrm{2}+\mathrm{8}+\mathrm{6}\right) \\ $$$$\:\:\:{S}=\mathrm{24}\:{sq}.{units}\:.\: \\ $$
Commented by mrW1 last updated on 12/Jun/17

$$\mathrm{24}\:\mathrm{is}\:\mathrm{correct}! \\ $$
Commented by ajfour last updated on 23/May/18
$${thanks}\:{Sir}.\:{What}\:{a}\:{nice}\:{question}, \\ $$$${Sir},\:{where}\:{do}\:{you}\:{get}\:{them}\:{from}? \\ $$
