Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

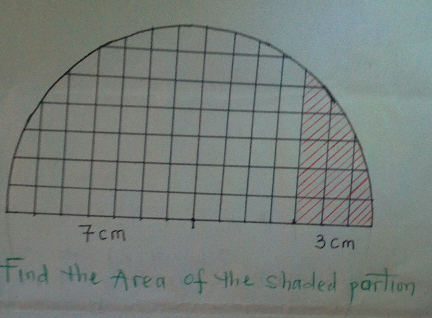
Question Number 15623 by tawa tawa last updated on 12/Jun/17

Answered by ajfour last updated on 12/Jun/17

Commented by ajfour last updated on 12/Jun/17

BD^2 =BC^( 2) −CD^2 AC=BC= r =7 h^2 = 49−16=33 h=(√(33)) . Area of ΔBCD=(1/2)×4×(√(33)) Area of sector ABC =(1/2)r^2 θ cos θ=(4/7) ⇒ θ=cos^(−1) ((4/7)) Shaded area = Area of sector ABC −Area of ΔBCD = (1/2)(7)^2 cos^(−1) ((4/7))−2(√(33)) Shaded area =((49)/2)cos^(−1) ((4/7))−2(√(33)) ≈ 12.093 .

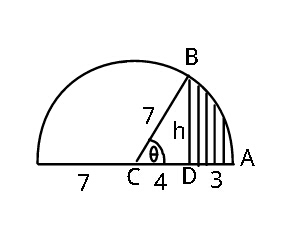
$$\:\:{BD}^{\mathrm{2}} ={BC}^{\:\mathrm{2}} −{CD}^{\mathrm{2}} \\ $$$$\:\:\:{AC}={BC}=\:{r}\:=\mathrm{7} \\ $$$$\:\:\:\:\:\:\:{h}^{\mathrm{2}} =\:\mathrm{49}−\mathrm{16}=\mathrm{33} \\ $$$$\:\:\:\:\:\:\:{h}=\sqrt{\mathrm{33}}\:. \\ $$$$\:{Area}\:{of}\:\Delta{BCD}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}×\sqrt{\mathrm{33}} \\ $$$$\:{Area}\:{of}\:{sector}\:{ABC}\:=\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:\:\mathrm{cos}\:\theta=\frac{\mathrm{4}}{\mathrm{7}}\:\Rightarrow\:\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{7}}\right) \\ $$$$\:{Shaded}\:{area}\:=\:{Area}\:{of}\:{sector}\:{ABC} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{Area}\:{of}\:\Delta{BCD} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{7}\right)^{\mathrm{2}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{7}}\right)−\mathrm{2}\sqrt{\mathrm{33}} \\ $$$${Shaded}\:{area}\:=\frac{\mathrm{49}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{7}}\right)−\mathrm{2}\sqrt{\mathrm{33}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\:\mathrm{12}.\mathrm{093}\:. \\ $$

Commented by tawa tawa last updated on 12/Jun/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com