
Question Number 155772 by daus last updated on 04/Oct/21

Answered by mr W last updated on 04/Oct/21
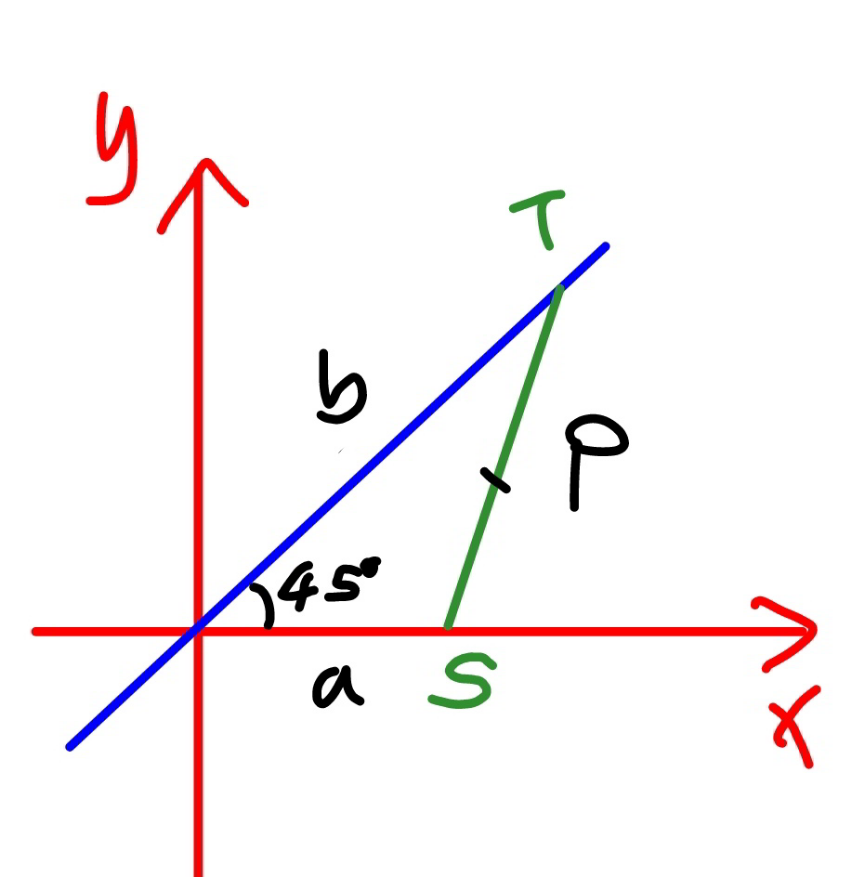
Commented by mr W last updated on 04/Oct/21
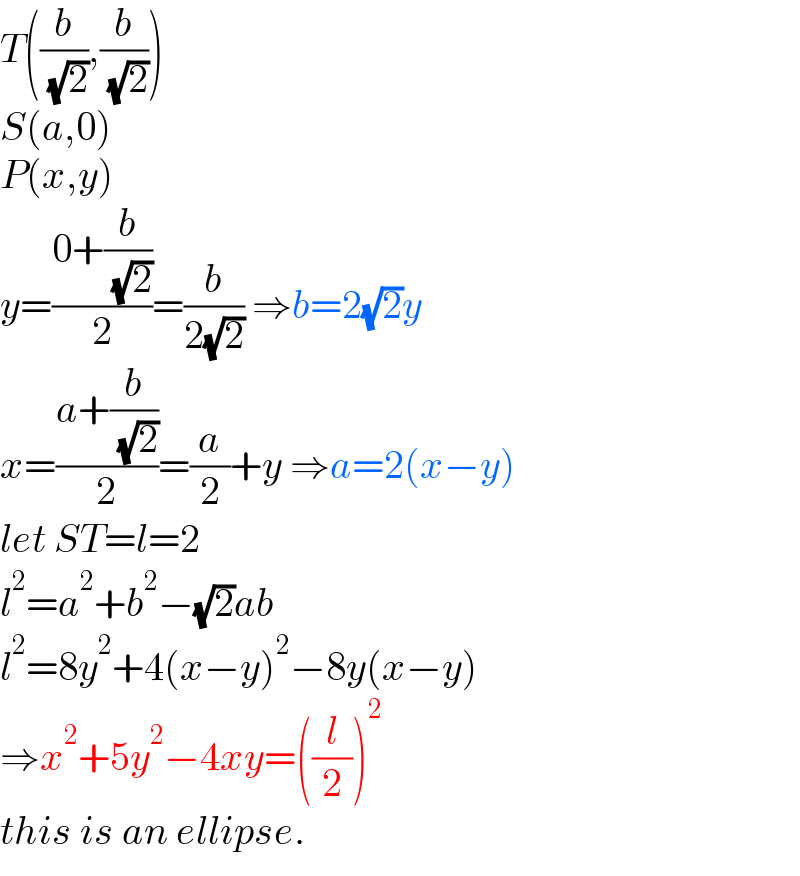
$${T}\left(\frac{{b}}{\:\sqrt{\mathrm{2}}},\frac{{b}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$${S}\left({a},\mathrm{0}\right) \\ $$$${P}\left({x},{y}\right) \\ $$$${y}=\frac{\mathrm{0}+\frac{{b}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}}=\frac{{b}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow{b}=\mathrm{2}\sqrt{\mathrm{2}}{y} \\ $$$${x}=\frac{{a}+\frac{{b}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}}=\frac{{a}}{\mathrm{2}}+{y}\:\Rightarrow{a}=\mathrm{2}\left({x}−{y}\right) \\ $$$${let}\:{ST}={l}=\mathrm{2} \\ $$$${l}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\sqrt{\mathrm{2}}{ab} \\ $$$${l}^{\mathrm{2}} =\mathrm{8}{y}^{\mathrm{2}} +\mathrm{4}\left({x}−{y}\right)^{\mathrm{2}} −\mathrm{8}{y}\left({x}−{y}\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{5}{y}^{\mathrm{2}} −\mathrm{4}{xy}=\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${this}\:{is}\:{an}\:{ellipse}. \\ $$
Commented by mr W last updated on 04/Oct/21
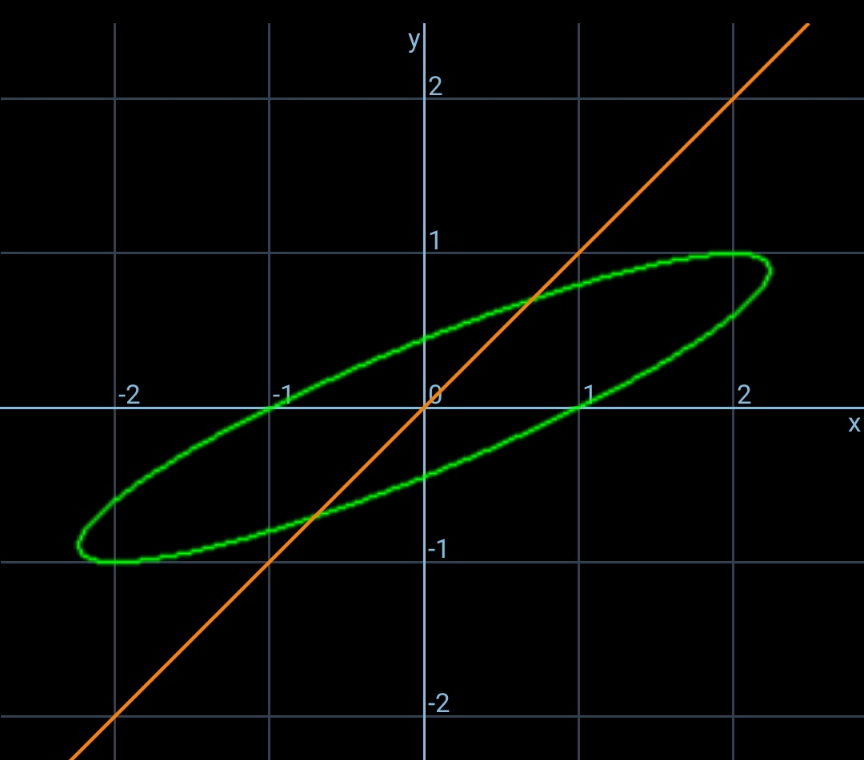
Commented by daus last updated on 05/Oct/21

$${thanks}\: \\ $$
