Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 154507 by RB95 last updated on 19/Sep/21

Commented by RB95 last updated on 19/Sep/21

Salut Aidez −moi svp urgent merci

$${Salut} \\ $$$${Aidez}\:−{moi}\:{svp} \\ $$$${urgent} \\ $$$${merci} \\ $$

Answered by Jonathanwaweh last updated on 19/Sep/21

1)p_n =Π_(k=1) ^n 2^k^2 lnp_n )=Σ_(k=1) ^n ln(2^k^2 ) =Σ_(k=1) ^n k^2 ln2=((n(n+1)(2n+1))/6)ln2=ln2^((n(n+1)(2n+6))/6) d′ou p_n =2^((n(n+1)(2n+6))/6) S_(n ) =Σ_(k=1) ^n ln(u_k )=Σk^2 ln2=((n(n+1)(2n+1))/6)ln2 2−a)v_(n+1) −v_n =(√(lnu_(n+1) ))−(√(lnu_n ))=(√(n+1)^2 ln2))−(√(n^2 ln2))=(n+1)(√(ln2))−n(√(ln2))=(√(ln2)) donc(v_n ) est une suite arithmetique de raison (√(ln2)) nature ona v_(k+1) −v_k =(√)ln2⇒Σ_(k=1) ^(n−1) (v_(k+1) −v_k )=(√(ln2))Σ_(k=1) ^(n−1) 1⇔v_n −v_1 =(n−1)(√(ln2)) en fesant tendre la limite on voit que (v_n ) est une suite divergente

$$\left.\mathrm{1}\left.\right){p}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{2}^{{k}^{\mathrm{2}} } \:\:\:\:\:{lnp}_{{n}} \right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left(\mathrm{2}^{{k}^{\mathrm{2}} } \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} {ln}\mathrm{2}=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}{ln}\mathrm{2}={ln}\mathrm{2}^{\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{6}\right)}{\mathrm{6}}} \\ $$$${d}'{ou}\:{p}_{{n}} =\mathrm{2}^{\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{6}\right)}{\mathrm{6}}} \\ $$$${S}_{{n}\:} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left({u}_{{k}} \right)=\Sigma{k}^{\mathrm{2}} {ln}\mathrm{2}=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}{ln}\mathrm{2} \\ $$$$\left.\mathrm{2}−{a}\right){v}_{{n}+\mathrm{1}} −{v}_{{n}} =\sqrt{{lnu}_{{n}+\mathrm{1}} }−\sqrt{{lnu}_{{n}} }=\sqrt{\left.{n}+\mathrm{1}\right)^{\mathrm{2}} {ln}\mathrm{2}}−\sqrt{{n}^{\mathrm{2}} {ln}\mathrm{2}}=\left({n}+\mathrm{1}\right)\sqrt{{ln}\mathrm{2}}−{n}\sqrt{{ln}\mathrm{2}}=\sqrt{{ln}\mathrm{2}}\:{donc}\left({v}_{{n}} \right)\:{est}\:{une}\:{suite}\:{arithmetique}\:{de}\:{raison}\:\sqrt{{ln}\mathrm{2}} \\ $$$${nature}\:{ona}\:{v}_{{k}+\mathrm{1}} −{v}_{{k}} =\sqrt{}{ln}\mathrm{2}\Rightarrow\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left({v}_{{k}+\mathrm{1}} −{v}_{{k}} \right)=\sqrt{{ln}\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{1}\Leftrightarrow{v}_{{n}} −{v}_{\mathrm{1}} =\left({n}−\mathrm{1}\right)\sqrt{{ln}\mathrm{2}}\:{en}\:{fesant}\:{tendre}\:{la}\:{limite}\:{on}\:{voit}\:{que}\:\left({v}_{{n}} \right)\:{est}\:{une}\:{suite}\:{divergente}\: \\ $$$$ \\ $$$$ \\ $$

Commented by RB95 last updated on 19/Sep/21

Merci!

Answered by Jonathanwaweh last updated on 19/Sep/21

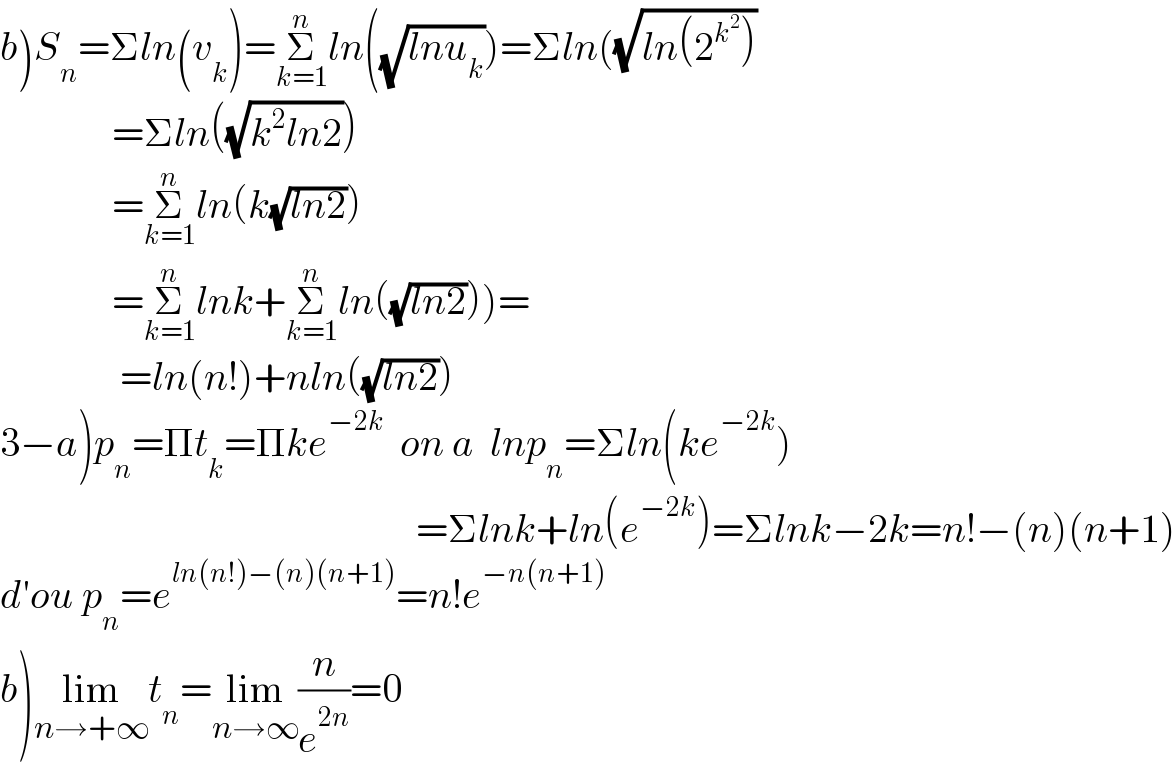
b)S_n =Σln(v_k )=Σ_(k=1) ^n ln((√(lnu_k )))=Σln((√(ln(2^k^2 ))) =Σln((√(k^2 ln2))) =Σ_(k=1) ^n ln(k(√(ln2))) =Σ_(k=1) ^n lnk+Σ_(k=1) ^n ln((√(ln2))))= =ln(n!)+nln((√(ln2))) 3−a)p_n =Πt_k =Πke^(−2k) on a lnp_n =Σln(ke^(−2k) ) =Σlnk+ln(e^(−2k) )=Σlnk−2k=n!−(n)(n+1) d′ou p_n =e^(ln(n!)−(n)(n+1)) =n!e^(−n(n+1)) b)lim_(n→+∞) t_n =lim_(n→∞) (n/e^(2n) )=0

$$\left.{b}\right){S}_{{n}} =\Sigma{ln}\left({v}_{{k}} \right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left(\sqrt{{lnu}_{{k}} }\right)=\Sigma{ln}\left(\sqrt{{ln}\left(\mathrm{2}^{{k}^{\mathrm{2}} } \right)}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\Sigma{ln}\left(\sqrt{{k}^{\mathrm{2}} {ln}\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left({k}\sqrt{{ln}\mathrm{2}}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{lnk}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left(\sqrt{{ln}\mathrm{2}}\right)\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ln}\left({n}!\right)+{nln}\left(\sqrt{{ln}\mathrm{2}}\right) \\ $$$$\left.\mathrm{3}−{a}\right){p}_{{n}} =\Pi{t}_{{k}} =\Pi{ke}^{−\mathrm{2}{k}} \:\:{on}\:{a}\:\:{lnp}_{{n}} =\Sigma{ln}\left({ke}^{−\mathrm{2}{k}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\Sigma{lnk}+{ln}\left({e}^{−\mathrm{2}{k}} \right)=\Sigma{lnk}−\mathrm{2}{k}={n}!−\left({n}\right)\left({n}+\mathrm{1}\right) \\ $$$${d}'{ou}\:{p}_{{n}} ={e}^{{ln}\left({n}!\right)−\left({n}\right)\left({n}+\mathrm{1}\right)} ={n}!{e}^{−{n}\left({n}+\mathrm{1}\right)} \\ $$$$\left.{b}\right)\underset{{n}\rightarrow+\infty} {\mathrm{lim}}{t}_{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}}{{e}^{\mathrm{2}{n}} }=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com