Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 154343 by Lekhraj last updated on 17/Sep/21

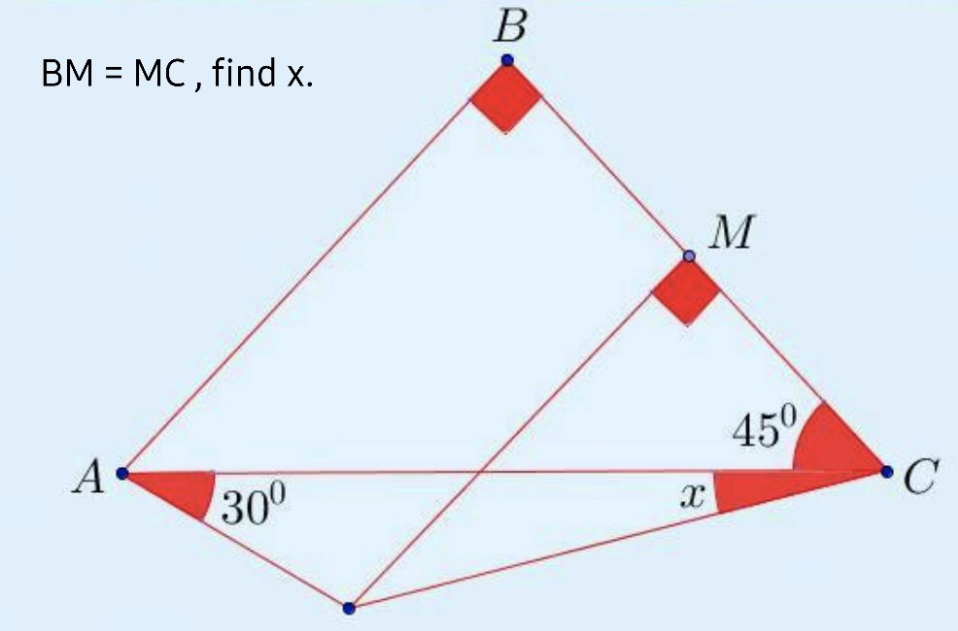
Answered by qaz last updated on 17/Sep/21

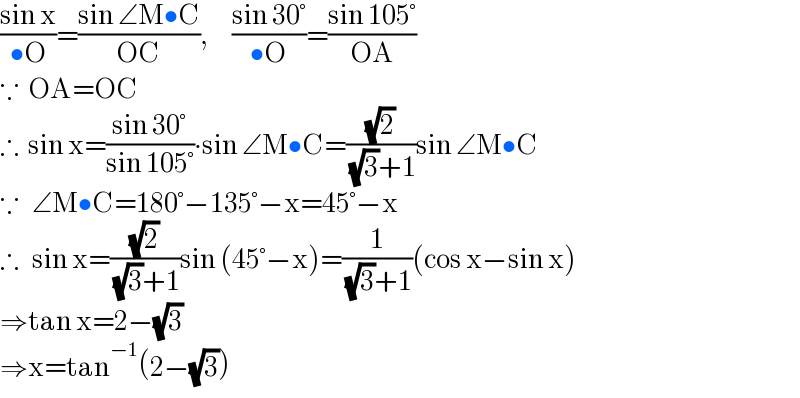
((sin x)/(•O))=((sin ∠M•C)/(OC)), ((sin 30°)/(•O))=((sin 105°)/(OA)) ∵ OA=OC ∴ sin x=((sin 30°)/(sin 105°))∙sin ∠M•C=((√2)/( (√3)+1))sin ∠M•C ∵ ∠M•C=180°−135°−x=45°−x ∴ sin x=((√2)/( (√3)+1))sin (45°−x)=(1/( (√3)+1))(cos x−sin x) ⇒tan x=2−(√3) ⇒x=tan^(−1) (2−(√3))

$$\frac{\mathrm{sin}\:\mathrm{x}}{\bullet\mathrm{O}}=\frac{\mathrm{sin}\:\angle\mathrm{M}\bullet\mathrm{C}}{\mathrm{OC}},\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{30}°}{\bullet\mathrm{O}}=\frac{\mathrm{sin}\:\mathrm{105}°}{\mathrm{OA}} \\ $$$$\because\:\:\mathrm{OA}=\mathrm{OC}\:\:\:\:\:\: \\ $$$$\therefore\:\:\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{sin}\:\mathrm{30}°}{\mathrm{sin}\:\mathrm{105}°}\centerdot\mathrm{sin}\:\angle\mathrm{M}\bullet\mathrm{C}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\mathrm{sin}\:\angle\mathrm{M}\bullet\mathrm{C} \\ $$$$\because\:\:\:\angle\mathrm{M}\bullet\mathrm{C}=\mathrm{180}°−\mathrm{135}°−\mathrm{x}=\mathrm{45}°−\mathrm{x} \\ $$$$\therefore\:\:\:\mathrm{sin}\:\mathrm{x}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\mathrm{sin}\:\left(\mathrm{45}°−\mathrm{x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\left(\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{x}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$

Commented by Lekhraj last updated on 17/Sep/21

Thank you . You does not mark in the figure which point is the blue dot and which point is o.

$$\:\mathrm{Thank}\:\mathrm{you}\:.\:\mathrm{You}\:\mathrm{does}\:\mathrm{not}\:\mathrm{mark}\:\mathrm{in}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{which}\:\mathrm{point}\:\mathrm{is}\:\mathrm{the}\:\mathrm{blue}\:\mathrm{dot} \\ $$$$\mathrm{and}\:\mathrm{which}\:\mathrm{point}\:\mathrm{is}\:\mathrm{o}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com