Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

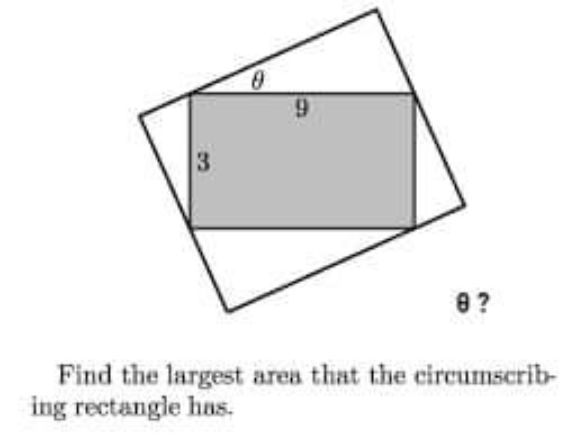
Question Number 154089 by iloveisrael last updated on 14/Sep/21

Answered by talminator2856791 last updated on 14/Sep/21

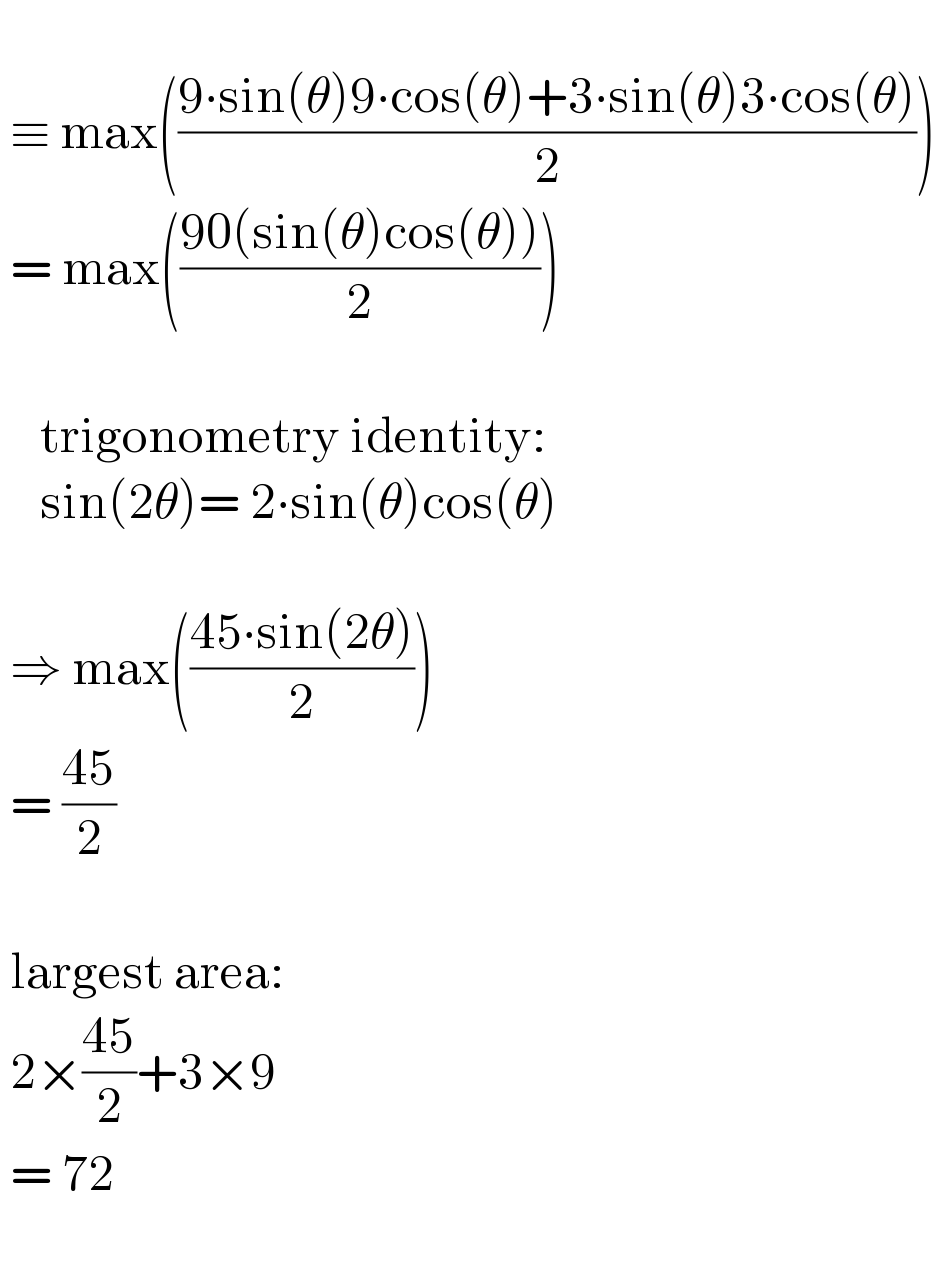
≡ max(((9∙sin(θ)9∙cos(θ)+3∙sin(θ)3∙cos(θ))/2)) = max(((90(sin(θ)cos(θ)))/2)) trigonometry identity: sin(2θ)= 2∙sin(θ)cos(θ) ⇒ max(((45∙sin(2θ))/2)) = ((45)/2) largest area: 2×((45)/2)+3×9 = 72

$$\: \\ $$$$\:\equiv\:\mathrm{max}\left(\frac{\mathrm{9}\centerdot\mathrm{sin}\left(\theta\right)\mathrm{9}\centerdot\mathrm{cos}\left(\theta\right)+\mathrm{3}\centerdot\mathrm{sin}\left(\theta\right)\mathrm{3}\centerdot\mathrm{cos}\left(\theta\right)}{\mathrm{2}}\right) \\ $$$$\:=\:\mathrm{max}\left(\frac{\mathrm{90}\left(\mathrm{sin}\left(\theta\right)\mathrm{cos}\left(\theta\right)\right)}{\mathrm{2}}\right) \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\mathrm{trigonometry}\:\mathrm{identity}: \\ $$$$\:\:\:\:\mathrm{sin}\left(\mathrm{2}\theta\right)=\:\mathrm{2}\centerdot\mathrm{sin}\left(\theta\right)\mathrm{cos}\left(\theta\right) \\ $$$$\: \\ $$$$\:\Rightarrow\:\mathrm{max}\left(\frac{\mathrm{45}\centerdot\mathrm{sin}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\right) \\ $$$$\:=\:\frac{\mathrm{45}}{\mathrm{2}} \\ $$$$\: \\ $$$$\:\mathrm{largest}\:\mathrm{area}: \\ $$$$\:\mathrm{2}×\frac{\mathrm{45}}{\mathrm{2}}+\mathrm{3}×\mathrm{9} \\ $$$$\:=\:\mathrm{72} \\ $$$$\: \\ $$

Answered by mr W last updated on 14/Sep/21

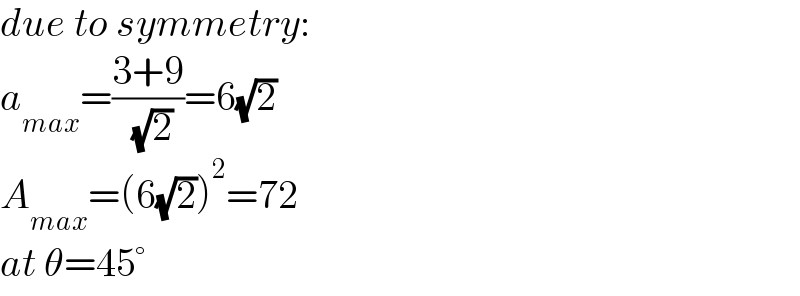
due to symmetry: a_(max) =((3+9)/( (√2)))=6(√2) A_(max) =(6(√2))^2 =72 at θ=45°

$${due}\:{to}\:{symmetry}: \\ $$$${a}_{{max}} =\frac{\mathrm{3}+\mathrm{9}}{\:\sqrt{\mathrm{2}}}=\mathrm{6}\sqrt{\mathrm{2}} \\ $$$${A}_{{max}} =\left(\mathrm{6}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{72} \\ $$$${at}\:\theta=\mathrm{45}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com