
Question Number 153905 by liberty last updated on 12/Sep/21

Commented by MJS_new last updated on 12/Sep/21
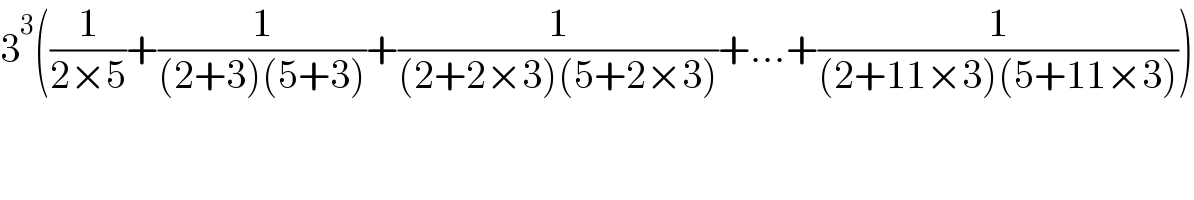
$$\mathrm{3}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}×\mathrm{5}}+\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{3}\right)\left(\mathrm{5}+\mathrm{3}\right)}+\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{2}×\mathrm{3}\right)\left(\mathrm{5}+\mathrm{2}×\mathrm{3}\right)}+...+\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{11}×\mathrm{3}\right)\left(\mathrm{5}+\mathrm{11}×\mathrm{3}\right)}\right) \\ $$
Answered by MJS_new last updated on 12/Sep/21

$$\frac{\mathrm{81}}{\mathrm{19}} \\ $$
Commented by liberty last updated on 12/Sep/21

$${how}? \\ $$
Answered by som(math1967) last updated on 12/Sep/21
![A=3^2 ((3/(2×5)) +(3/(5×8)) +(3/(8×11)) ...+(3/(35×38))) =3^2 ((1/2) −(1/5)+(1/5)−(1/8)+(1/8)−(1/(11))+...(1/(35))−(1/(38))] =3^2 ×((1/2)−(1/(38)))=9×((18)/(38))=((81)/(19))](Q153913.png)
$$\boldsymbol{{A}}=\mathrm{3}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}×\mathrm{5}}\:+\frac{\mathrm{3}}{\mathrm{5}×\mathrm{8}}\:+\frac{\mathrm{3}}{\mathrm{8}×\mathrm{11}}\:...+\frac{\mathrm{3}}{\mathrm{35}×\mathrm{38}}\right) \\ $$$$\:=\mathrm{3}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{11}}+...\frac{\mathrm{1}}{\mathrm{35}}−\frac{\mathrm{1}}{\mathrm{38}}\right] \\ $$$$=\mathrm{3}^{\mathrm{2}} ×\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{38}}\right)=\mathrm{9}×\frac{\mathrm{18}}{\mathrm{38}}=\frac{\mathrm{81}}{\mathrm{19}} \\ $$
Commented by liberty last updated on 12/Sep/21

$${wonderfull} \\ $$
Commented by puissant last updated on 12/Sep/21
Wow what a look ������
