Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 153611 by saly last updated on 08/Sep/21

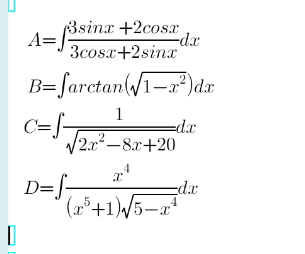
Answered by Ar Brandon last updated on 08/Sep/21

A=∫((3sinx+2cosx)/(3cosx+2sinx))dx =∫((2cosx−3sinx)/(2sinx+3cosx))dx+6∫((sinx)/(2sinx+3cosx))dx =ln∣2sinx+3cosx∣+6∫(((4t)/(1+t^2 ))/(((4t)/(1+t^2 ))+3((1−t^2 )/(1+t^2 ))))∙(dt/(1+t^2 )) =ln∣2sinx+3cosx∣+6∫((4tdt)/((3+4t−3t^2 )(1+t^2 ))) You may proceed with the decomposition ((4t)/((3t^2 −4t−3)(t^2 +1)))=((at+b)/(3t^2 −4t−3))+((ct+d)/(t^2 +1))

$${A}=\int\frac{\mathrm{3sin}{x}+\mathrm{2cos}{x}}{\mathrm{3cos}{x}+\mathrm{2sin}{x}}{dx} \\ $$$$\:\:\:\:=\int\frac{\mathrm{2cos}{x}−\mathrm{3sin}{x}}{\mathrm{2sin}{x}+\mathrm{3cos}{x}}{dx}+\mathrm{6}\int\frac{\mathrm{sin}{x}}{\mathrm{2sin}{x}+\mathrm{3cos}{x}}{dx} \\ $$$$\:\:\:\:=\mathrm{ln}\mid\mathrm{2sin}{x}+\mathrm{3cos}{x}\mid+\mathrm{6}\int\frac{\frac{\mathrm{4}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{4}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{3}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\centerdot\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\mathrm{ln}\mid\mathrm{2sin}{x}+\mathrm{3cos}{x}\mid+\mathrm{6}\int\frac{\mathrm{4}{tdt}}{\left(\mathrm{3}+\mathrm{4}{t}−\mathrm{3}{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\mathrm{You}\:\mathrm{may}\:\mathrm{proceed}\:\mathrm{with}\:\mathrm{the}\:\mathrm{decomposition} \\ $$$$\frac{\mathrm{4}{t}}{\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}{t}−\mathrm{3}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{at}+{b}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}{t}−\mathrm{3}}+\frac{{ct}+{d}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$

Commented by saly last updated on 08/Sep/21

Thank you But in number B.C.D ?

$$\:\:{Thank}\:{you} \\ $$$$\:\:\:{But}\:{in}\:{number}\:\:{B}.{C}.{D}\:? \\ $$

Answered by Ar Brandon last updated on 08/Sep/21

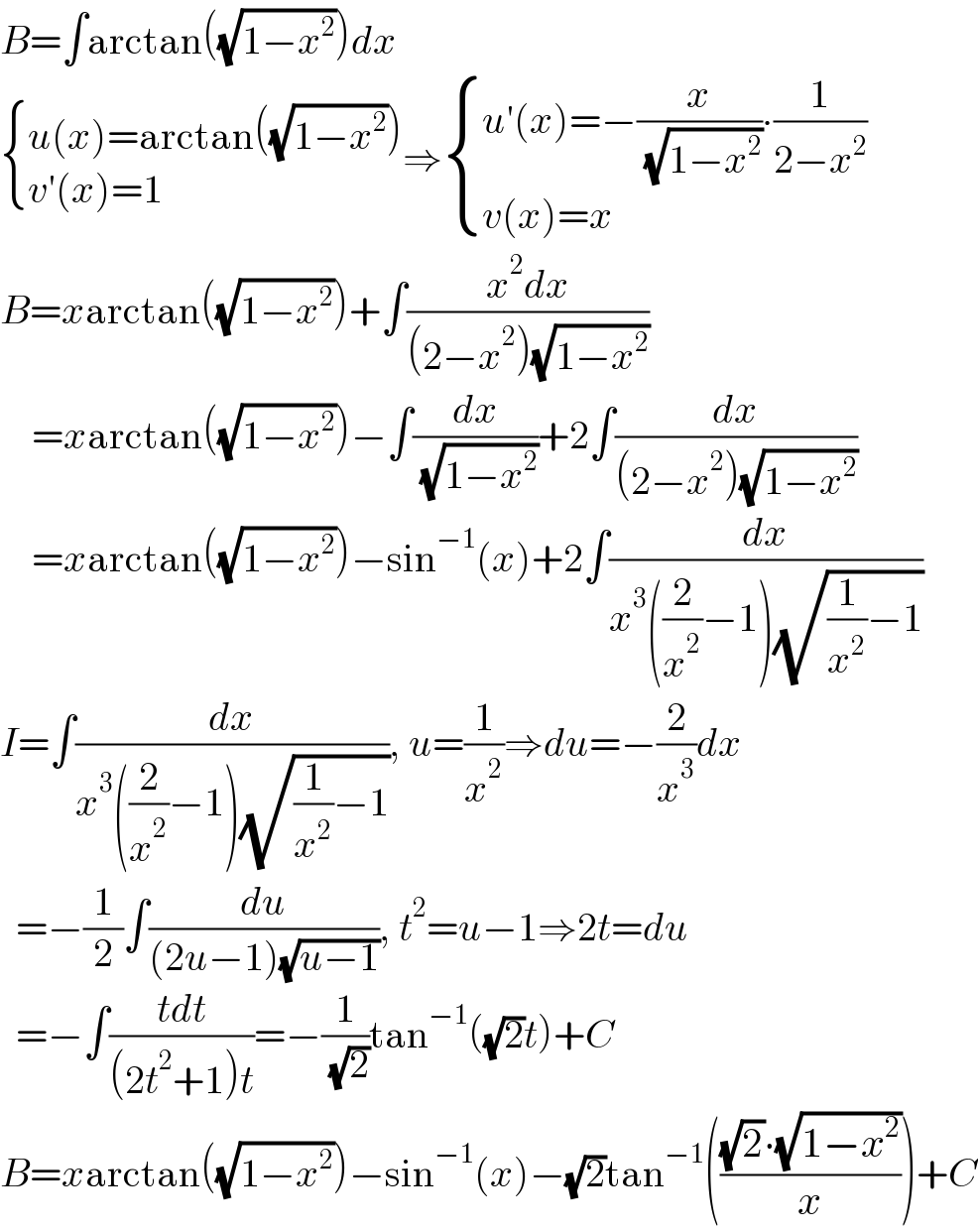
B=∫arctan((√(1−x^2 )))dx { ((u(x)=arctan((√(1−x^2 ))))),((v′(x)=1)) :}⇒ { ((u′(x)=−(x/( (√(1−x^2 ))))∙(1/(2−x^2 )))),((v(x)=x)) :} B=xarctan((√(1−x^2 )))+∫((x^2 dx)/((2−x^2 )(√(1−x^2 )))) =xarctan((√(1−x^2 )))−∫(dx/( (√(1−x^2 ))))+2∫(dx/((2−x^2 )(√(1−x^2 )))) =xarctan((√(1−x^2 )))−sin^(−1) (x)+2∫(dx/(x^3 ((2/x^2 )−1)(√((1/x^2 )−1)))) I=∫(dx/(x^3 ((2/x^2 )−1)(√((1/x^2 )−1)))), u=(1/x^2 )⇒du=−(2/x^3 )dx =−(1/2)∫(du/((2u−1)(√(u−1)))), t^2 =u−1⇒2t=du =−∫((tdt)/((2t^2 +1)t))=−(1/( (√2)))tan^(−1) ((√2)t)+C B=xarctan((√(1−x^2 )))−sin^(−1) (x)−(√2)tan^(−1) ((((√2)∙(√(1−x^2 )))/x))+C

$${B}=\int\mathrm{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx} \\ $$$$\begin{cases}{{u}\left({x}\right)=\mathrm{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}\\{{v}'\left({x}\right)=\mathrm{1}}\end{cases}\Rightarrow\begin{cases}{{u}'\left({x}\right)=−\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\centerdot\frac{\mathrm{1}}{\mathrm{2}−{x}^{\mathrm{2}} }}\\{{v}\left({x}\right)={x}}\end{cases} \\ $$$${B}={x}\mathrm{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)+\int\frac{{x}^{\mathrm{2}} {dx}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\:\:\:\:={x}\mathrm{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\mathrm{2}\int\frac{{dx}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\:\:\:\:={x}\mathrm{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−\mathrm{sin}^{−\mathrm{1}} \left({x}\right)+\mathrm{2}\int\frac{{dx}}{{x}^{\mathrm{3}} \left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} }−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}} \\ $$$${I}=\int\frac{{dx}}{{x}^{\mathrm{3}} \left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} }−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}},\:{u}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\Rightarrow{du}=−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }{dx} \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{\left(\mathrm{2}{u}−\mathrm{1}\right)\sqrt{{u}−\mathrm{1}}},\:{t}^{\mathrm{2}} ={u}−\mathrm{1}\Rightarrow\mathrm{2}{t}={du} \\ $$$$\:\:=−\int\frac{{tdt}}{\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right){t}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{t}\right)+{C} \\ $$$${B}={x}\mathrm{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−\mathrm{sin}^{−\mathrm{1}} \left({x}\right)−\sqrt{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}\centerdot\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\right)+{C} \\ $$

Answered by Ar Brandon last updated on 08/Sep/21

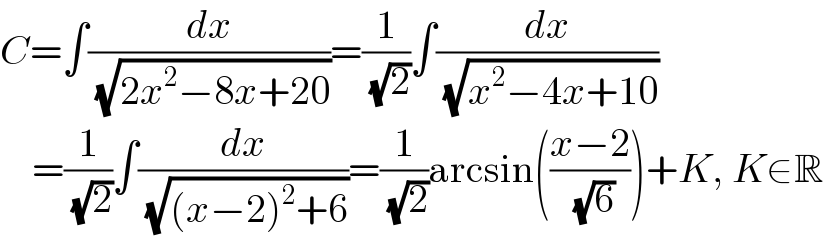
C=∫(dx/( (√(2x^2 −8x+20))))=(1/( (√2)))∫(dx/( (√(x^2 −4x+10)))) =(1/( (√2)))∫(dx/( (√((x−2)^2 +6))))=(1/( (√2)))arcsin(((x−2)/( (√6))))+K, K∈R

$${C}=\int\frac{{dx}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{20}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{10}}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dx}}{\:\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{6}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arcsin}\left(\frac{{x}−\mathrm{2}}{\:\sqrt{\mathrm{6}}}\right)+{K},\:{K}\in\mathbb{R} \\ $$

Commented by saly last updated on 08/Sep/21

Thank you very much

$$\:\:{Thank}\:\:{you}\:{very}\:{much} \\ $$

Commented by Ar Brandon last updated on 08/Sep/21

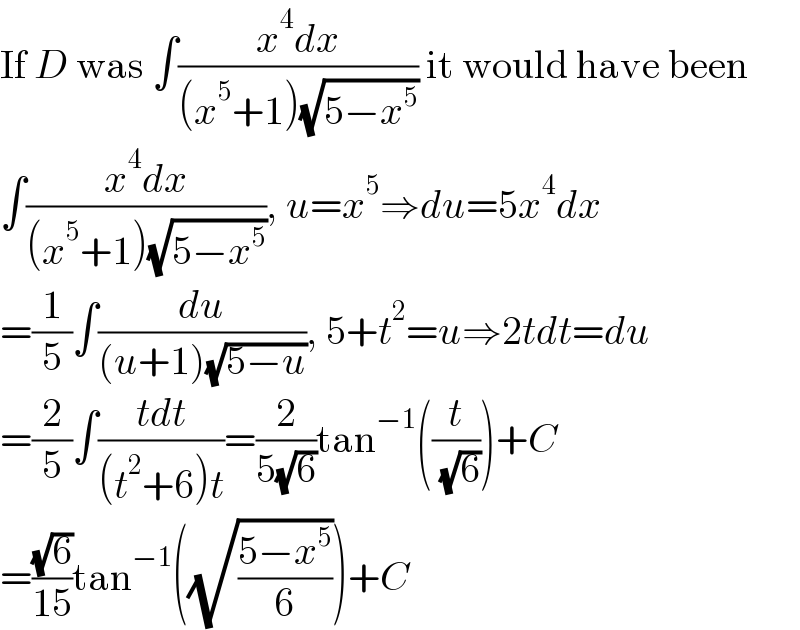
If D was ∫((x^4 dx)/((x^5 +1)(√(5−x^5 )))) it would have been ∫((x^4 dx)/((x^5 +1)(√(5−x^5 )))), u=x^5 ⇒du=5x^4 dx =(1/5)∫(du/((u+1)(√(5−u)))), 5+t^2 =u⇒2tdt=du =(2/5)∫((tdt)/((t^2 +6)t))=(2/(5(√6)))tan^(−1) ((t/( (√6))))+C =((√6)/(15))tan^(−1) ((√((5−x^5 )/6)))+C

$$\mathrm{If}\:{D}\:\mathrm{was}\:\int\frac{{x}^{\mathrm{4}} {dx}}{\left({x}^{\mathrm{5}} +\mathrm{1}\right)\sqrt{\mathrm{5}−{x}^{\mathrm{5}} }}\:\mathrm{it}\:\mathrm{would}\:\mathrm{have}\:\mathrm{been} \\ $$$$\int\frac{{x}^{\mathrm{4}} {dx}}{\left({x}^{\mathrm{5}} +\mathrm{1}\right)\sqrt{\mathrm{5}−{x}^{\mathrm{5}} }},\:{u}={x}^{\mathrm{5}} \Rightarrow{du}=\mathrm{5}{x}^{\mathrm{4}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{du}}{\left({u}+\mathrm{1}\right)\sqrt{\mathrm{5}−{u}}},\:\mathrm{5}+{t}^{\mathrm{2}} ={u}\Rightarrow\mathrm{2}{tdt}={du} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\int\frac{{tdt}}{\left({t}^{\mathrm{2}} +\mathrm{6}\right){t}}=\frac{\mathrm{2}}{\mathrm{5}\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{t}}{\:\sqrt{\mathrm{6}}}\right)+{C} \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{15}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{5}−{x}^{\mathrm{5}} }{\mathrm{6}}}\right)+{C} \\ $$

Commented by Ar Brandon last updated on 08/Sep/21

You're welcome

Commented by puissant last updated on 08/Sep/21

sacré Brandon ������������

Commented by Ar Brandon last updated on 08/Sep/21

Bonsoir bro

Terms of Service

Privacy Policy

Contact: info@tinkutara.com