
Question Number 153537 by SANOGO last updated on 08/Sep/21
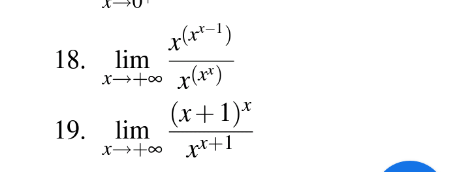
Answered by puissant last updated on 08/Sep/21

$$\left.\mathrm{18}\right) \\ $$$${on}\:{remarque}\:{d}'{abord}\:{que} \\ $$$${x}^{{x}} =\mathrm{1}+{xlnx}+....+\frac{\left({xlnx}\right)^{{n}} }{{n}!}\left(\mathrm{1}+\varepsilon\left({x}\right)\right) \\ $$$$\varepsilon\left({x}\right)\rightarrow\mathrm{0}\:{quand}\:{x}\rightarrow\mathrm{0} \\ $$$${alors}\:{posons}\:{une}\:{suite}\:{U}_{{k}} \left({x}\right)=\frac{\left({xlnx}\right)^{{k}} }{{k}!} \\ $$$${pour}\:{k}\in\mathbb{N}. \\ $$$${on}\:{remarque}\:{que}\:{chaque}\:{U}_{{k}−\mathrm{1}} {est} \\ $$$${n}\acute {{e}gligeable}\:{devant}\:{U}_{{k}} \\ $$$${alors}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{U}_{{k}−\mathrm{1}} }{{U}_{{k}} }\right)=\mathrm{0} \\ $$$${alors}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\left({x}^{{x}−\mathrm{1}} \right)} }{{x}^{\left({x}^{{x}} \right)} }\:=\:\mathrm{0} \\ $$$$\left.\mathrm{19}\right) \\ $$$${On}\:{remarque}\:{aussi}\:{que}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)^{{x}} }{{x}^{{x}+\mathrm{1}} }=\mathrm{0} \\ $$
