Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 152993 by 7770 last updated on 03/Sep/21

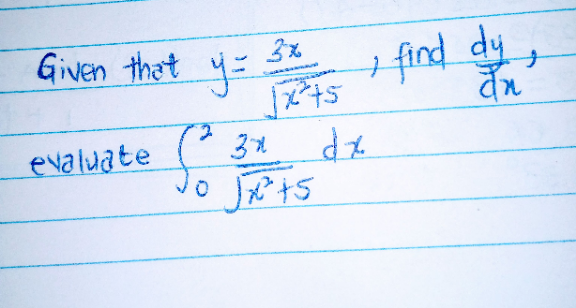
Commented by otchereabdullai@gmail.com last updated on 08/Sep/21

nice

$$\mathrm{nice} \\ $$

Answered by bobhans last updated on 04/Sep/21

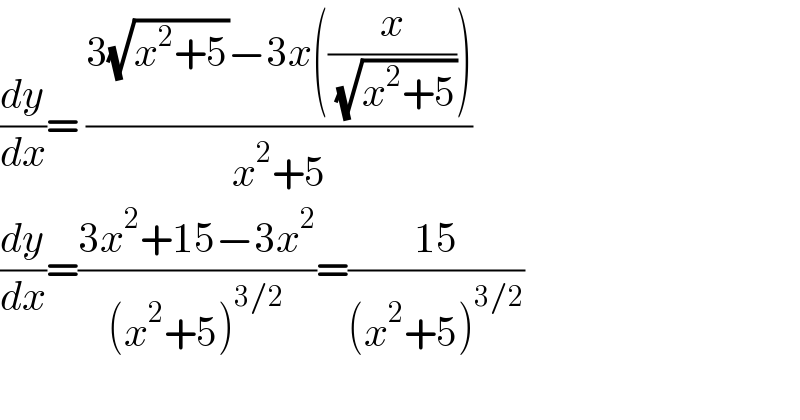
(dy/dx)= ((3(√(x^2 +5))−3x((x/( (√(x^2 +5))))))/(x^2 +5)) (dy/dx)=((3x^2 +15−3x^2 )/((x^2 +5)^(3/2) ))=((15)/((x^2 +5)^(3/2) ))

$$\frac{{dy}}{{dx}}=\:\frac{\mathrm{3}\sqrt{{x}^{\mathrm{2}} +\mathrm{5}}−\mathrm{3}{x}\left(\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{5}}}\right)}{{x}^{\mathrm{2}} +\mathrm{5}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{15}−\mathrm{3}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{3}/\mathrm{2}} }=\frac{\mathrm{15}}{\left({x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$ \\ $$

Answered by bobhans last updated on 04/Sep/21

(2)∫_0 ^2 ((3x)/( (√(x^2 +5)))) dx =(3/2)∫_(√5) ^3 (du/( (√u))) =(3/2)[ 2(√u) ]_(√5) ^3 = 3(√3)−3(5)^(1/4)

$$\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{3}{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{5}}}\:{dx}\:=\frac{\mathrm{3}}{\mathrm{2}}\int_{\sqrt{\mathrm{5}}} ^{\mathrm{3}} \frac{{du}}{\:\sqrt{{u}}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{2}}\left[\:\mathrm{2}\sqrt{{u}}\:\right]_{\sqrt{\mathrm{5}}} ^{\mathrm{3}} \:=\:\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt[{\mathrm{4}}]{\mathrm{5}}\: \\ $$

Answered by hoochhoch last updated on 04/Sep/21

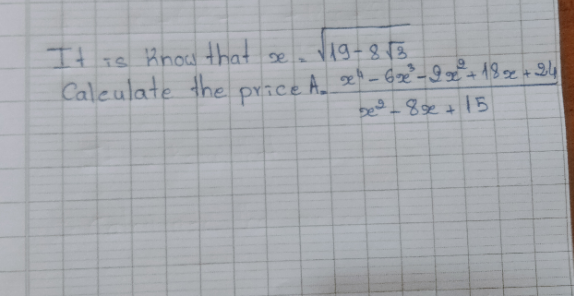
Commented by benhamimed last updated on 04/Sep/21

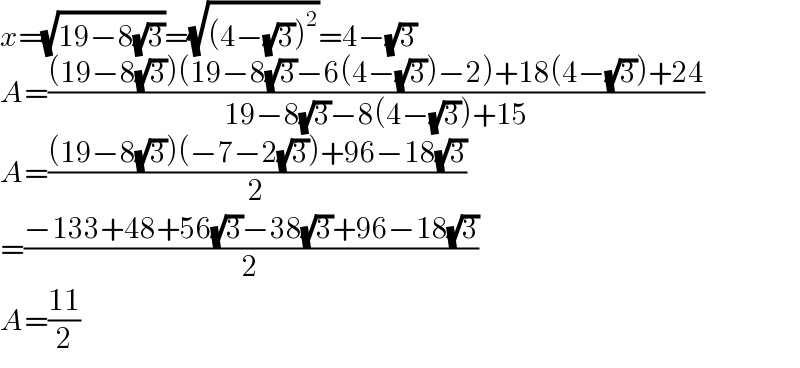
x=(√(19−8(√3)))=(√((4−(√3))^2 ))=4−(√3) A=(((19−8(√3))(19−8(√3)−6(4−(√3))−2)+18(4−(√3))+24)/(19−8(√3)−8(4−(√3))+15)) A=(((19−8(√3))(−7−2(√3))+96−18(√3))/2) =((−133+48+56(√3)−38(√3)+96−18(√3))/2) A=((11)/2)

$${x}=\sqrt{\mathrm{19}−\mathrm{8}\sqrt{\mathrm{3}}}=\sqrt{\left(\mathrm{4}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{4}−\sqrt{\mathrm{3}} \\ $$$${A}=\frac{\left(\mathrm{19}−\mathrm{8}\sqrt{\mathrm{3}}\right)\left(\mathrm{19}−\mathrm{8}\sqrt{\mathrm{3}}−\mathrm{6}\left(\mathrm{4}−\sqrt{\mathrm{3}}\right)−\mathrm{2}\right)+\mathrm{18}\left(\mathrm{4}−\sqrt{\mathrm{3}}\right)+\mathrm{24}}{\mathrm{19}−\mathrm{8}\sqrt{\mathrm{3}}−\mathrm{8}\left(\mathrm{4}−\sqrt{\mathrm{3}}\right)+\mathrm{15}} \\ $$$${A}=\frac{\left(\mathrm{19}−\mathrm{8}\sqrt{\mathrm{3}}\right)\left(−\mathrm{7}−\mathrm{2}\sqrt{\mathrm{3}}\right)+\mathrm{96}−\mathrm{18}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{−\mathrm{133}+\mathrm{48}+\mathrm{56}\sqrt{\mathrm{3}}−\mathrm{38}\sqrt{\mathrm{3}}+\mathrm{96}−\mathrm{18}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${A}=\frac{\mathrm{11}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com