
Question Number 152974 by Rankut last updated on 03/Sep/21
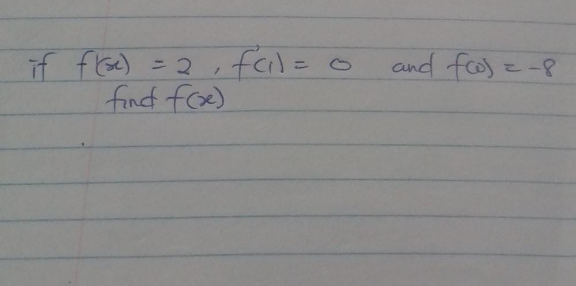
Commented by Rankut last updated on 03/Sep/21

$${help} \\ $$
Commented by mr W last updated on 03/Sep/21
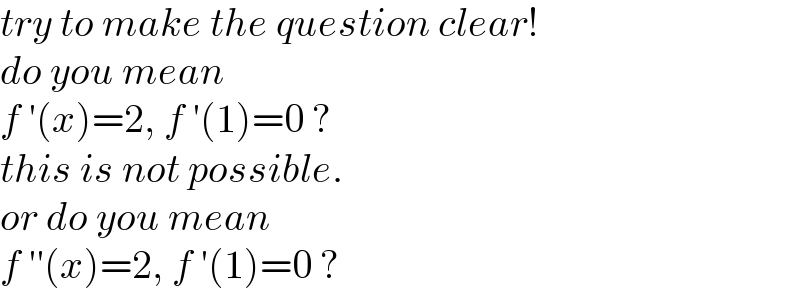
$${try}\:{to}\:{make}\:{the}\:{question}\:{clear}! \\ $$$${do}\:{you}\:{mean} \\ $$$${f}\:'\left({x}\right)=\mathrm{2},\:{f}\:'\left(\mathrm{1}\right)=\mathrm{0}\:?\: \\ $$$${this}\:{is}\:{not}\:{possible}. \\ $$$${or}\:{do}\:{you}\:{mean} \\ $$$${f}\:''\left({x}\right)=\mathrm{2},\:{f}\:'\left(\mathrm{1}\right)=\mathrm{0}\:?\: \\ $$
Commented by Rankut last updated on 03/Sep/21

$${yes}\:{please} \\ $$$${f}\:''\left({x}\right)=\mathrm{2},\:{f}\:'\left(\mathrm{1}\right)=\mathrm{0} \\ $$
Commented by mr W last updated on 03/Sep/21
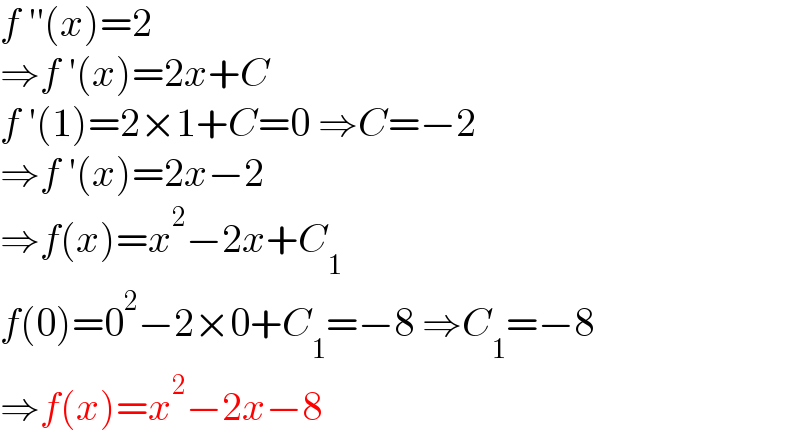
$${f}\:''\left({x}\right)=\mathrm{2} \\ $$$$\Rightarrow{f}\:'\left({x}\right)=\mathrm{2}{x}+{C} \\ $$$${f}\:'\left(\mathrm{1}\right)=\mathrm{2}×\mathrm{1}+{C}=\mathrm{0}\:\Rightarrow{C}=−\mathrm{2} \\ $$$$\Rightarrow{f}\:'\left({x}\right)=\mathrm{2}{x}−\mathrm{2} \\ $$$$\Rightarrow{f}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{2}{x}+{C}_{\mathrm{1}} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}^{\mathrm{2}} −\mathrm{2}×\mathrm{0}+{C}_{\mathrm{1}} =−\mathrm{8}\:\Rightarrow{C}_{\mathrm{1}} =−\mathrm{8} \\ $$$$\Rightarrow{f}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{8} \\ $$
Commented by amin96 last updated on 03/Sep/21

$$ \\ $$Write as clearly as possible. the image is unclear
Commented by 7770 last updated on 04/Sep/21

$${thank}\:{you}\:{sir} \\ $$
