Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 152903 by DELETED last updated on 03/Sep/21

Answered by DELETED last updated on 03/Sep/21

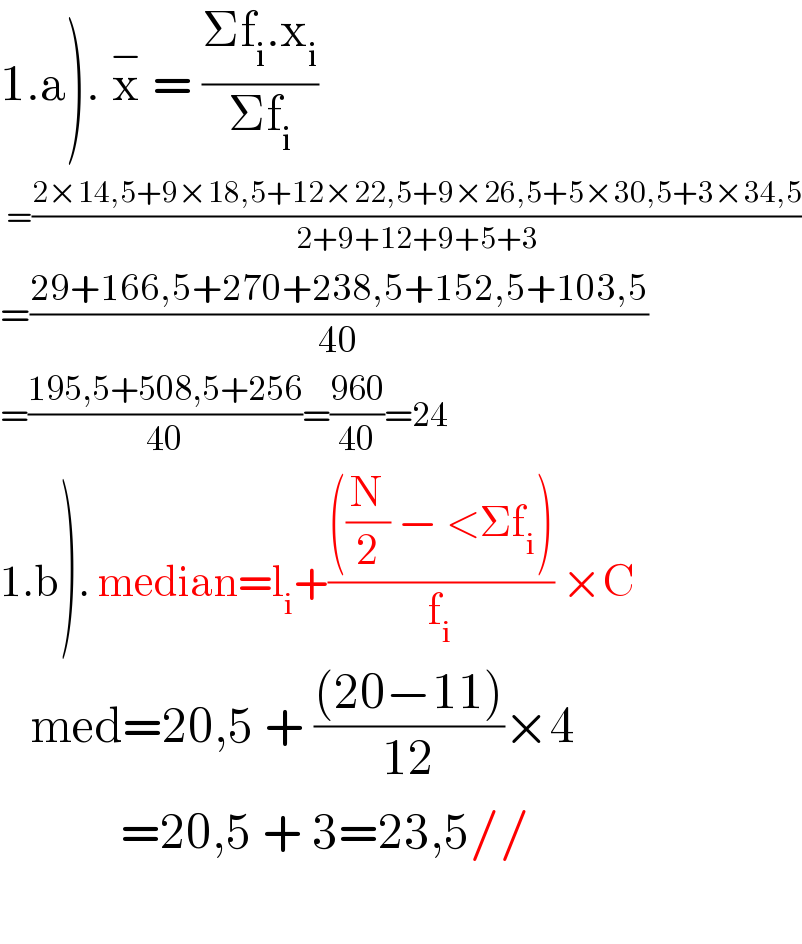
1.a). x^− = ((Σf_i .x_i )/(Σf_i )) =((2×14,5+9×18,5+12×22,5+9×26,5+5×30,5+3×34,5)/(2+9+12+9+5+3)) =((29+166,5+270+238,5+152,5+103,5)/(40)) =((195,5+508,5+256)/(40))=((960)/(40))=24 1.b). median=l_i +((((N/2) − <Σf_i ))/f_i ) ×C med=20,5 + (((20−11))/(12))×4 =20,5 + 3=23,5//

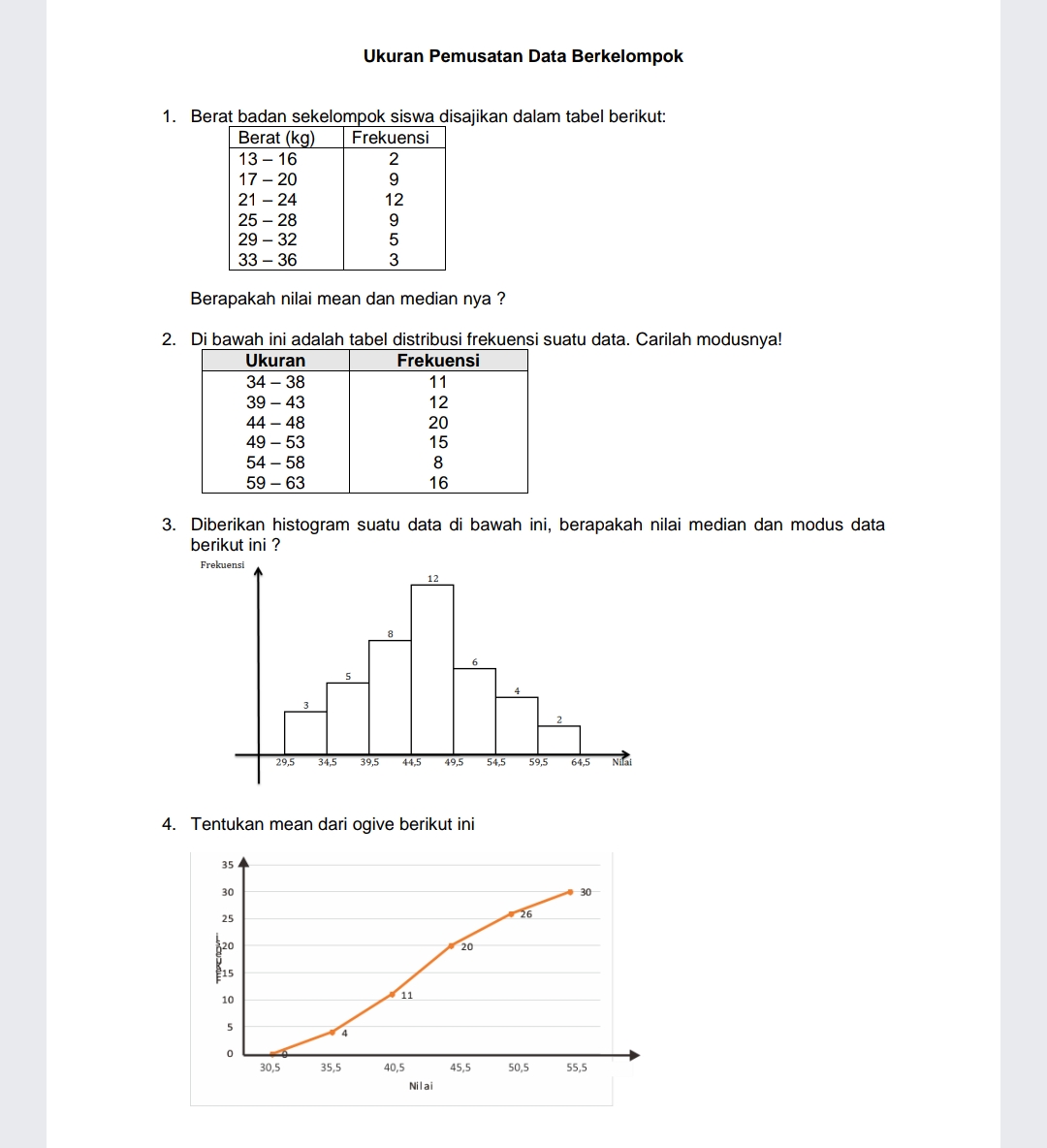
$$\left.\mathrm{1}.\mathrm{a}\right).\:\overset{−} {\mathrm{x}}\:=\:\frac{\Sigma\mathrm{f}_{\mathrm{i}} .\mathrm{x}_{\mathrm{i}} }{\Sigma\mathrm{f}_{\mathrm{i}} }\: \\ $$$$\:=\frac{\mathrm{2}×\mathrm{14},\mathrm{5}+\mathrm{9}×\mathrm{18},\mathrm{5}+\mathrm{12}×\mathrm{22},\mathrm{5}+\mathrm{9}×\mathrm{26},\mathrm{5}+\mathrm{5}×\mathrm{30},\mathrm{5}+\mathrm{3}×\mathrm{34},\mathrm{5}}{\mathrm{2}+\mathrm{9}+\mathrm{12}+\mathrm{9}+\mathrm{5}+\mathrm{3}} \\ $$$$=\frac{\mathrm{29}+\mathrm{166},\mathrm{5}+\mathrm{270}+\mathrm{238},\mathrm{5}+\mathrm{152},\mathrm{5}+\mathrm{103},\mathrm{5}}{\mathrm{40}} \\ $$$$=\frac{\mathrm{195},\mathrm{5}+\mathrm{508},\mathrm{5}+\mathrm{256}}{\mathrm{40}}=\frac{\mathrm{960}}{\mathrm{40}}=\mathrm{24} \\ $$$$\left.\mathrm{1}.\mathrm{b}\right).\:\mathrm{median}=\mathrm{l}_{\mathrm{i}} +\frac{\left(\frac{\mathrm{N}}{\mathrm{2}}\:−\:<\Sigma\mathrm{f}_{\mathrm{i}} \right)}{\mathrm{f}_{\mathrm{i}} }\:×\mathrm{C} \\ $$$$\:\:\:\mathrm{med}=\mathrm{20},\mathrm{5}\:+\:\frac{\left(\mathrm{20}−\mathrm{11}\right)}{\mathrm{12}}×\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{20},\mathrm{5}\:+\:\mathrm{3}=\mathrm{23},\mathrm{5}// \\ $$$$ \\ $$

Answered by DELETED last updated on 03/Sep/21

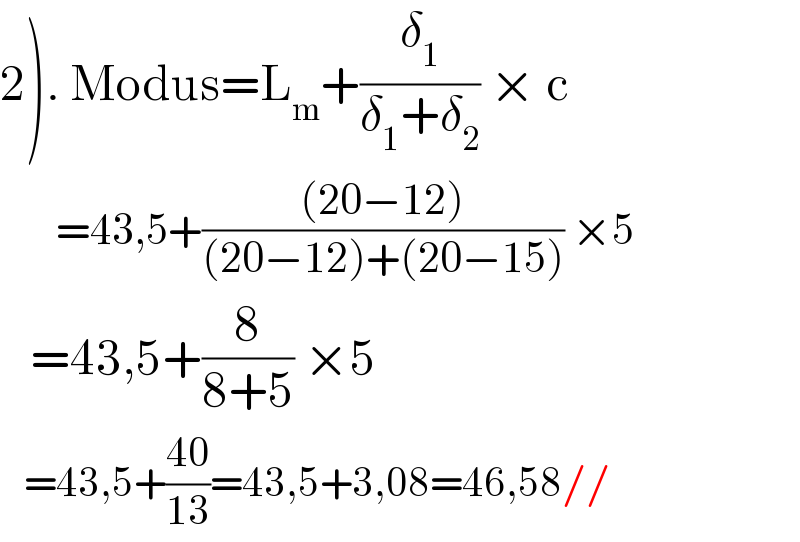
2). Modus=L_m +(δ_1 /(δ_1 +δ_2 )) × c =43,5+(((20−12))/((20−12)+(20−15))) ×5 =43,5+(8/(8+5)) ×5 =43,5+((40)/(13))=43,5+3,08=46,58//

$$\left.\mathrm{2}\right).\:\mathrm{Modus}=\mathrm{L}_{\mathrm{m}} +\frac{\delta_{\mathrm{1}} }{\delta_{\mathrm{1}} +\delta_{\mathrm{2}} }\:×\:\mathrm{c} \\ $$$$\:\:\:\:\:\:\:=\mathrm{43},\mathrm{5}+\frac{\left(\mathrm{20}−\mathrm{12}\right)}{\left(\mathrm{20}−\mathrm{12}\right)+\left(\mathrm{20}−\mathrm{15}\right)}\:×\mathrm{5} \\ $$$$\:\:\:=\mathrm{43},\mathrm{5}+\frac{\mathrm{8}}{\mathrm{8}+\mathrm{5}}\:×\mathrm{5} \\ $$$$\:\:\:=\mathrm{43},\mathrm{5}+\frac{\mathrm{40}}{\mathrm{13}}=\mathrm{43},\mathrm{5}+\mathrm{3},\mathrm{08}=\mathrm{46},\mathrm{58}// \\ $$

Answered by DELETED last updated on 03/Sep/21

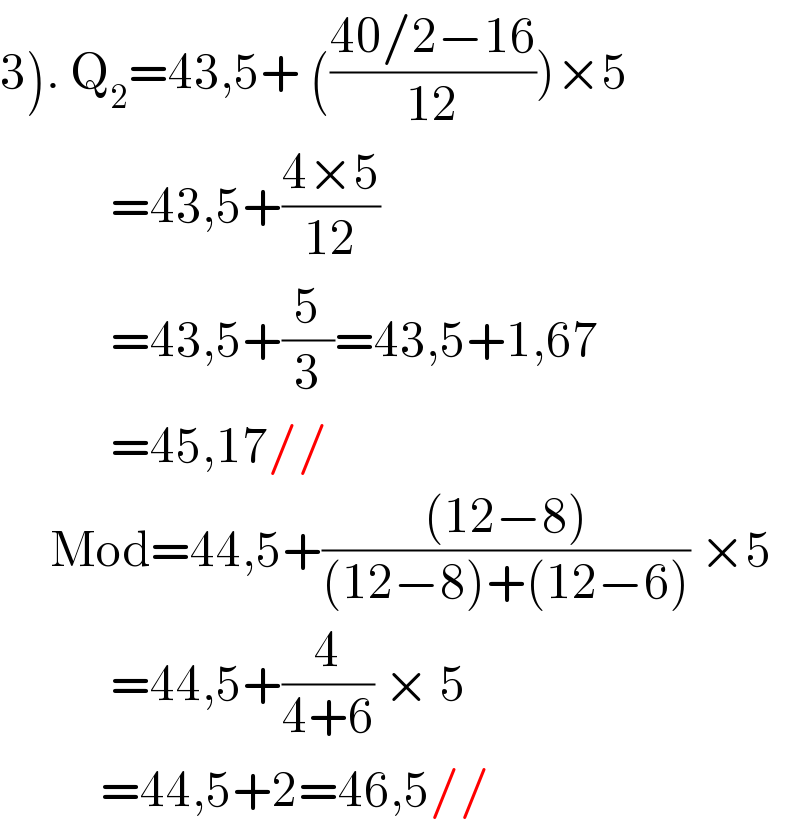
3). Q_2 =43,5+ (((40/2−16)/(12)))×5 =43,5+((4×5)/(12)) =43,5+(5/3)=43,5+1,67 =45,17// Mod=44,5+(((12−8))/((12−8)+(12−6))) ×5 =44,5+(4/(4+6)) × 5 =44,5+2=46,5//

$$\left.\mathrm{3}\right).\:\mathrm{Q}_{\mathrm{2}} =\mathrm{43},\mathrm{5}+\:\left(\frac{\mathrm{40}/\mathrm{2}−\mathrm{16}}{\mathrm{12}}\right)×\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{43},\mathrm{5}+\frac{\mathrm{4}×\mathrm{5}}{\mathrm{12}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{43},\mathrm{5}+\frac{\mathrm{5}}{\mathrm{3}}=\mathrm{43},\mathrm{5}+\mathrm{1},\mathrm{67} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{45},\mathrm{17}// \\ $$$$\:\:\:\:\:\mathrm{Mod}=\mathrm{44},\mathrm{5}+\frac{\left(\mathrm{12}−\mathrm{8}\right)}{\left(\mathrm{12}−\mathrm{8}\right)+\left(\mathrm{12}−\mathrm{6}\right)}\:×\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{44},\mathrm{5}+\frac{\mathrm{4}}{\mathrm{4}+\mathrm{6}}\:×\:\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{44},\mathrm{5}+\mathrm{2}=\mathrm{46},\mathrm{5}// \\ $$

Answered by DELETED last updated on 03/Sep/21

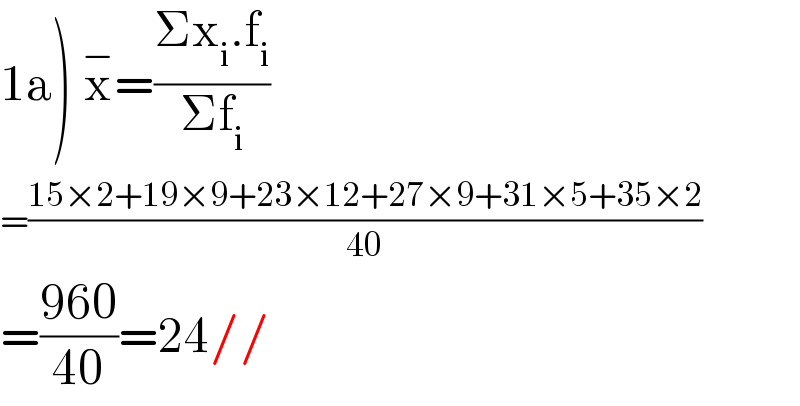
1a) x^− =((Σx_i .f_i )/(Σf_i )) =((15×2+19×9+23×12+27×9+31×5+35×2)/(40)) =((960)/(40))=24//

$$\left.\mathrm{1a}\right)\:\overset{−} {\mathrm{x}}=\frac{\Sigma\mathrm{x}_{\mathrm{i}} .\mathrm{f}_{\mathrm{i}} }{\Sigma\mathrm{f}_{\mathrm{i}} }\: \\ $$$$=\frac{\mathrm{15}×\mathrm{2}+\mathrm{19}×\mathrm{9}+\mathrm{23}×\mathrm{12}+\mathrm{27}×\mathrm{9}+\mathrm{31}×\mathrm{5}+\mathrm{35}×\mathrm{2}}{\mathrm{40}} \\ $$$$=\frac{\mathrm{960}}{\mathrm{40}}=\mathrm{24}// \\ $$

Answered by DELETED last updated on 03/Sep/21

Soal no 2 Rumus modus: M_o =L_i +((δ_1 /(δ_1 +δ_2 )))×C =(44−0.5)+(((20−12)/((20−12)+(20−15))))×5 =43,5+((8/(8+5)))×5 =43,5+((40)/(13))=43,5+3,08 =46,58//

$$\mathrm{Soal}\:\mathrm{no}\:\mathrm{2} \\ $$$$\mathrm{Rumus}\:\mathrm{modus}: \\ $$$$\mathrm{M}_{\mathrm{o}} =\mathrm{L}_{\mathrm{i}} +\left(\frac{\delta_{\mathrm{1}} }{\delta_{\mathrm{1}} +\delta_{\mathrm{2}} }\right)×\mathrm{C} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{44}−\mathrm{0}.\mathrm{5}\right)+\left(\frac{\mathrm{20}−\mathrm{12}}{\left(\mathrm{20}−\mathrm{12}\right)+\left(\mathrm{20}−\mathrm{15}\right)}\right)×\mathrm{5} \\ $$$$\:\:\:\:=\mathrm{43},\mathrm{5}+\left(\frac{\mathrm{8}}{\mathrm{8}+\mathrm{5}}\right)×\mathrm{5} \\ $$$$\:\:\:\:=\mathrm{43},\mathrm{5}+\frac{\mathrm{40}}{\mathrm{13}}=\mathrm{43},\mathrm{5}+\mathrm{3},\mathrm{08} \\ $$$$\:\:\:\:=\mathrm{46},\mathrm{58}// \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com