
Question Number 152740 by mr W last updated on 31/Aug/21

Commented by mr W last updated on 31/Aug/21
![[Q152712]](Q152743.png)
$$\left[{Q}\mathrm{152712}\right] \\ $$
Answered by mr W last updated on 31/Aug/21

Commented by mr W last updated on 31/Aug/21
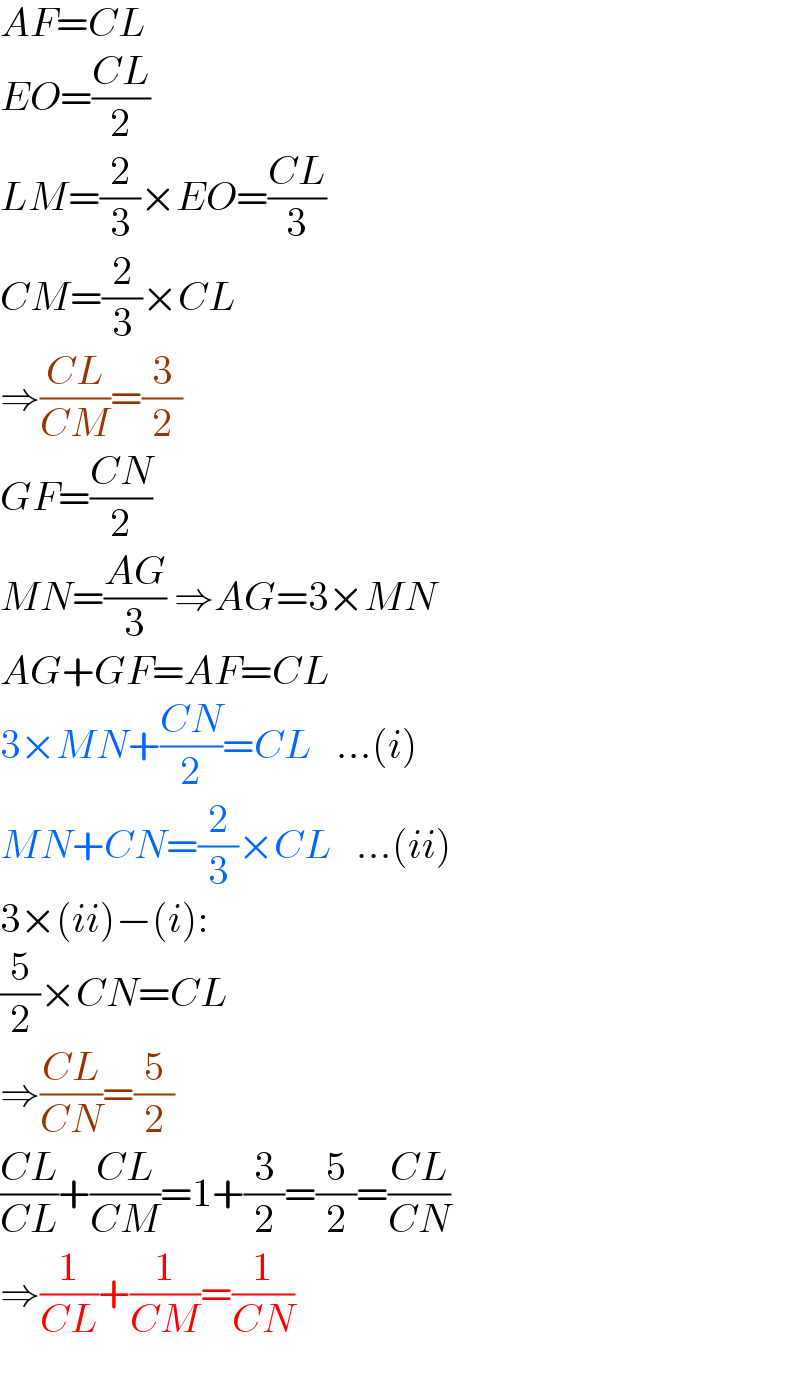
$${AF}={CL} \\ $$$${EO}=\frac{{CL}}{\mathrm{2}} \\ $$$${LM}=\frac{\mathrm{2}}{\mathrm{3}}×{EO}=\frac{{CL}}{\mathrm{3}} \\ $$$${CM}=\frac{\mathrm{2}}{\mathrm{3}}×{CL}\: \\ $$$$\Rightarrow\frac{{CL}}{{CM}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${GF}=\frac{{CN}}{\mathrm{2}} \\ $$$${MN}=\frac{{AG}}{\mathrm{3}}\:\Rightarrow{AG}=\mathrm{3}×{MN} \\ $$$${AG}+{GF}={AF}={CL} \\ $$$$\mathrm{3}×{MN}+\frac{{CN}}{\mathrm{2}}={CL}\:\:\:...\left({i}\right) \\ $$$${MN}+{CN}=\frac{\mathrm{2}}{\mathrm{3}}×{CL}\:\:\:...\left({ii}\right) \\ $$$$\mathrm{3}×\left({ii}\right)−\left({i}\right): \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}×{CN}={CL} \\ $$$$\Rightarrow\frac{{CL}}{{CN}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\frac{{CL}}{{CL}}+\frac{{CL}}{{CM}}=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}}=\frac{{CL}}{{CN}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{CL}}+\frac{\mathrm{1}}{{CM}}=\frac{\mathrm{1}}{{CN}} \\ $$
Commented by Tawa11 last updated on 31/Aug/21
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
