
Question Number 152377 by fotosy2k last updated on 27/Aug/21
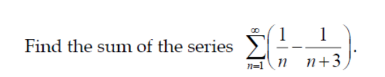
Commented by fotosy2k last updated on 28/Aug/21

$${pls}\:{help} \\ $$
Commented by Tawa11 last updated on 28/Aug/21

$$\mathrm{good} \\ $$
Answered by Mokmokhi last updated on 28/Aug/21
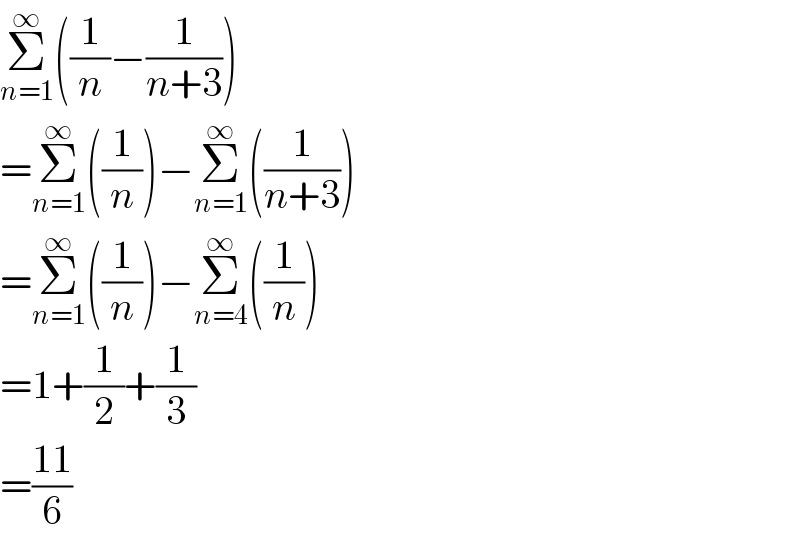
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right) \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}\right)−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\mathrm{3}}\right) \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}\right)−\underset{{n}=\mathrm{4}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{11}}{\mathrm{6}} \\ $$
Answered by Kamel last updated on 28/Aug/21
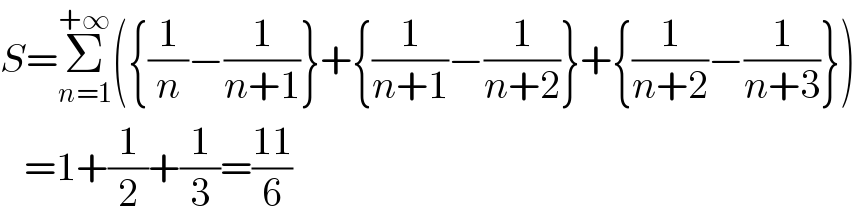
$${S}=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\left(\left\{\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\}+\left\{\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right\}+\left\{\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right\}\right) \\ $$$$\:\:\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{11}}{\mathrm{6}} \\ $$
Answered by qaz last updated on 28/Aug/21

$$\mathrm{H}_{\mathrm{3}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{11}}{\mathrm{6}} \\ $$
