
Question Number 152030 by mathdanisur last updated on 25/Aug/21
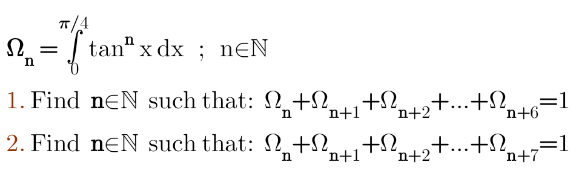
Commented by mathdanisur last updated on 26/Aug/21
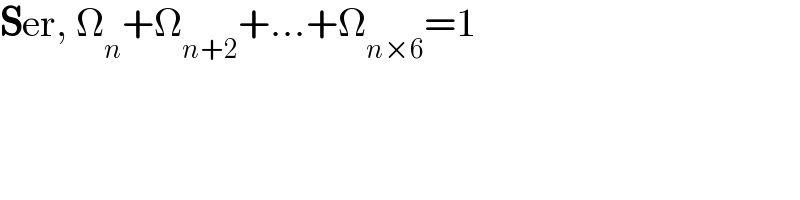
$$\boldsymbol{\mathrm{S}}\mathrm{er},\:\Omega_{{n}} +\Omega_{{n}+\mathrm{2}} +...+\Omega_{{n}×\mathrm{6}} =\mathrm{1} \\ $$
Commented by ghimisi last updated on 25/Aug/21
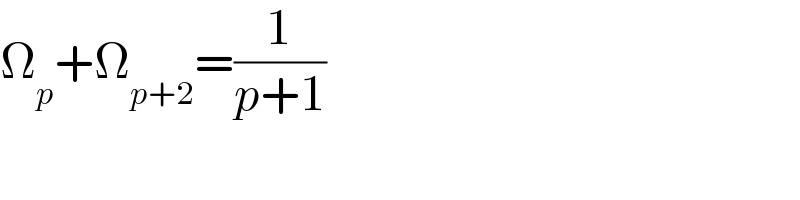
$$\Omega_{{p}} +\Omega_{{p}+\mathrm{2}} =\frac{\mathrm{1}}{{p}+\mathrm{1}} \\ $$
Answered by Kamel last updated on 25/Aug/21
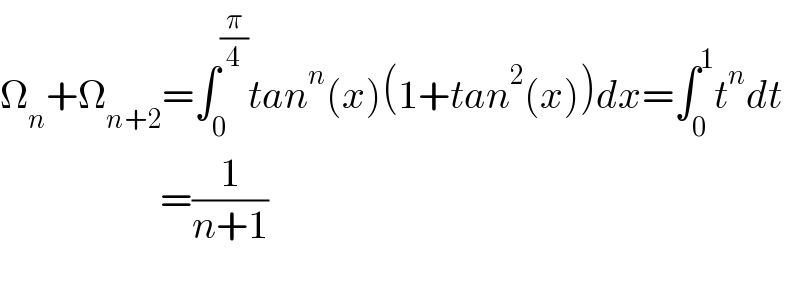
$$\Omega_{{n}} +\Omega_{{n}+\mathrm{2}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tan}^{{n}} \left({x}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 26/Aug/21
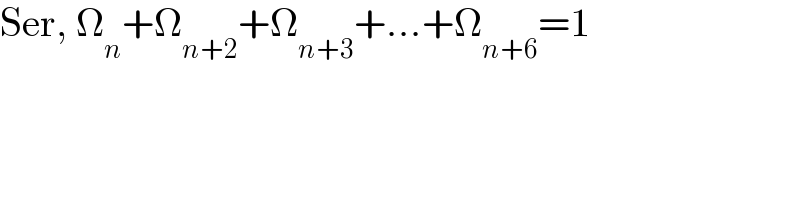
$$\mathrm{Ser},\:\Omega_{{n}} +\Omega_{{n}+\mathrm{2}} +\Omega_{{n}+\mathrm{3}} +...+\Omega_{{n}+\mathrm{6}} =\mathrm{1} \\ $$
