
Question Number 15170 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Jun/17

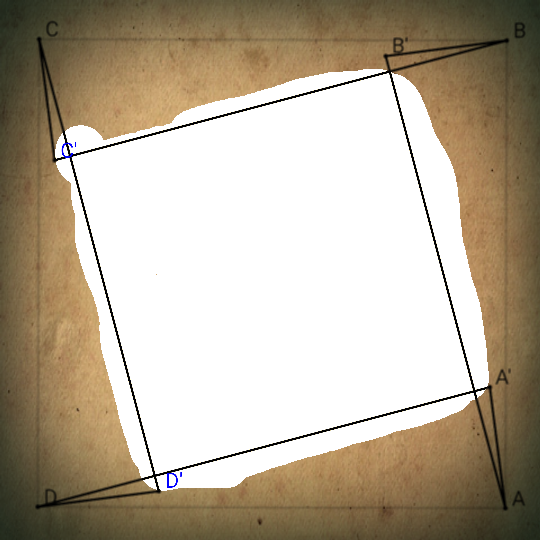
$${ABCD},{is}\:{a}\:{square}\:{with}\:{area}=\mathrm{1} \\ $$$${each}\:{acute}\:{angles}\:{such}\:{that}:\measuredangle{ADA}' \\ $$$${are}\:{equail}\:{to}:\mathrm{15}^{\bullet} \\ $$$$\left.\mathrm{1}\right){show}\:{that}\::{the}\:{white}\:{shape}\:{is}\:{a}\:{square}. \\ $$$$\left.\mathrm{2}\right){find}\:{it}'{s}\:{area}. \\ $$$$\left.\mathrm{3}\right){show}\:{that}:\:{DD}'\:{is}\:{the}\:{bisect}\:{of}\:\measuredangle{ADA}'. \\ $$$$\left.\mathrm{4}\right){find}\:{part}\:{of}\:{A}\overset{\Delta} {{D}A}'{s}\:{area}\:{that}\:{located} \\ $$$${on}\:{the}\:{right}\:{side}\:{of}\:{line}\:{AB}'. \\ $$
Commented by ajfour last updated on 08/Jun/17
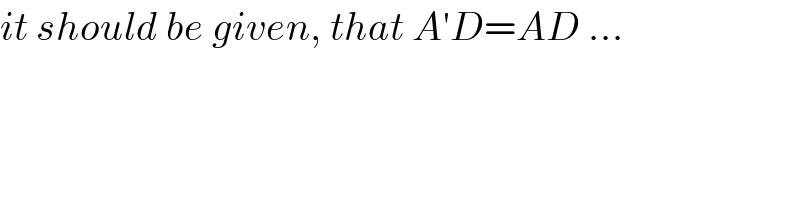
$${it}\:{should}\:{be}\:{given},\:{that}\:{A}'{D}={AD}\:... \\ $$
Answered by mrW1 last updated on 08/Jun/17

$$\mathrm{side}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{white}\:\mathrm{square}: \\ $$$$\mathrm{p}=\mathrm{1}×\mathrm{cos}\:\mathrm{15}°−\mathrm{1}×\mathrm{sin}\:\mathrm{15}° \\ $$$$=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{30}°}{\mathrm{2}}\:}−\:\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{30}°}{\mathrm{2}}} \\ $$$$=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}−\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{white}\:\mathrm{square}: \\ $$$$\mathrm{p}^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}−\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$ \\ $$$$\angle\mathrm{A}'\mathrm{AB}'=\frac{\mathrm{180}−\mathrm{15}}{\mathrm{2}}−\left(\mathrm{90}−\mathrm{15}\right)=\mathrm{7}.\mathrm{5}° \\ $$$$\Rightarrow\mathrm{A}'\mathrm{A}\:\mathrm{is}\:\mathrm{bisector}\:\mathrm{of}\:\angle\mathrm{BAB}' \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{M}=\mathrm{intersection}\:\mathrm{of}\:\mathrm{DA}'\:\mathrm{and}\:\mathrm{AB}' \\ $$$$\mathrm{A}'\mathrm{M}=\mathrm{DA}'−\mathrm{DM}=\mathrm{1}−\mathrm{cos}\:\mathrm{15}° \\ $$$$\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{AMA}' \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{A}'\mathrm{M}×\mathrm{AM}=\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{1}−\mathrm{cos}\:\mathrm{15}°\right)×\mathrm{sin}\:\mathrm{15}° \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{sin}\:\mathrm{15}°−\frac{\mathrm{sin}\:\mathrm{30}°}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}−\mathrm{1}}{\mathrm{8}}\approx\mathrm{0}.\mathrm{0044} \\ $$
Commented by mrW1 last updated on 08/Jun/17

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right},\:\mathrm{thanks}.\:\mathrm{it}\:\mathrm{is}\:\mathrm{fixed}\:\mathrm{now}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 08/Jun/17
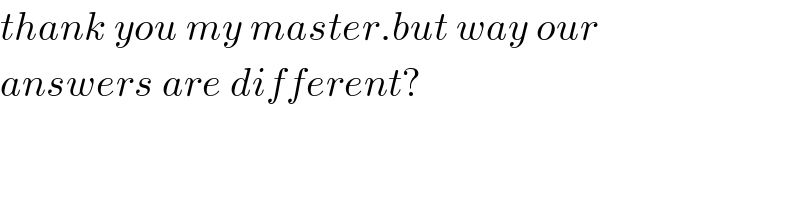
$${thank}\:{you}\:{my}\:{master}.{but}\:{way}\:{our}\: \\ $$$${answers}\:{are}\:{different}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 08/Jun/17
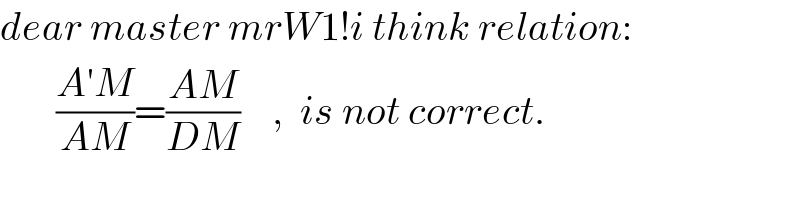
$${dear}\:{master}\:{mrW}\mathrm{1}!{i}\:{think}\:{relation}: \\ $$$$\:\:\:\:\:\:\:\frac{{A}'{M}}{{AM}}=\frac{{AM}}{{DM}}\:\:\:\:,\:\:{is}\:{not}\:{correct}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 08/Jun/17
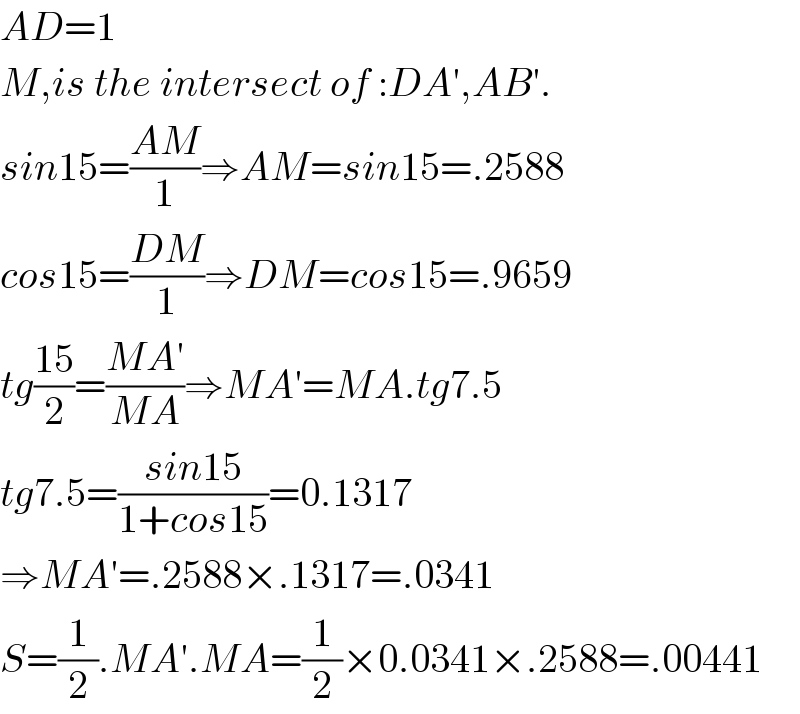
$${AD}=\mathrm{1} \\ $$$${M},{is}\:{the}\:{intersect}\:{of}\::{DA}',{AB}'. \\ $$$${sin}\mathrm{15}=\frac{{AM}}{\mathrm{1}}\Rightarrow{AM}={sin}\mathrm{15}=.\mathrm{2588} \\ $$$${cos}\mathrm{15}=\frac{{DM}}{\mathrm{1}}\Rightarrow{DM}={cos}\mathrm{15}=.\mathrm{9659} \\ $$$${tg}\frac{\mathrm{15}}{\mathrm{2}}=\frac{{MA}'}{{MA}}\Rightarrow{MA}'={MA}.{tg}\mathrm{7}.\mathrm{5} \\ $$$${tg}\mathrm{7}.\mathrm{5}=\frac{{sin}\mathrm{15}}{\mathrm{1}+{cos}\mathrm{15}}=\mathrm{0}.\mathrm{1317} \\ $$$$\Rightarrow{MA}'=.\mathrm{2588}×.\mathrm{1317}=.\mathrm{0341} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}.{MA}'.{MA}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}.\mathrm{0341}×.\mathrm{2588}=.\mathrm{00441} \\ $$
Commented by mrW1 last updated on 08/Jun/17

$$\mathrm{I}\:\mathrm{think}\:\mathrm{here}\:\mathrm{is}\:\mathrm{error} \\ $$$$ \\ $$$$\Rightarrow{MA}'=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}.\left(\mathrm{1}−\frac{\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\right)= \\ $$$$\neq\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\mathrm{1}\right)\:\:\left(\mathrm{error}\right) \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 08/Jun/17
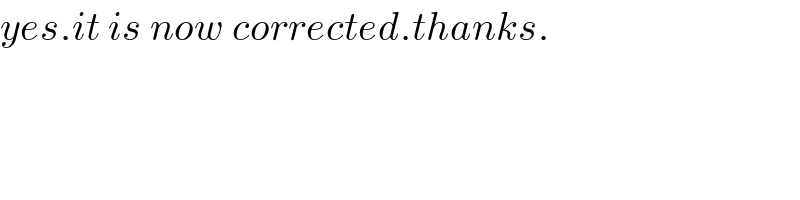
$${yes}.{it}\:{is}\:{now}\:{corrected}.{thanks}. \\ $$
