
Question Number 151104 by john_santu last updated on 18/Aug/21
Commented by john_santu last updated on 18/Aug/21
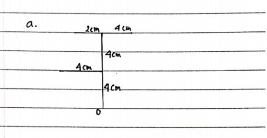
find the center of gravity with respect to point O
Answered by Olaf_Thorendsen last updated on 18/Aug/21

$$\bullet\:\mathrm{vertical} \\ $$$$\mathrm{L}_{\mathrm{1}} \:=\:\mathrm{8}\:\mathrm{cm} \\ $$$$\Omega_{\mathrm{1}} \left(\mathrm{0},\mathrm{4}\right) \\ $$$$ \\ $$$$\bullet\:\mathrm{lower}\:\mathrm{left} \\ $$$$\mathrm{L}_{\mathrm{2}} \:=\:\mathrm{4}\:\mathrm{cm} \\ $$$$\Omega_{\mathrm{2}} \left(−\mathrm{2},\mathrm{4}\right) \\ $$$$ \\ $$$$\bullet\:\mathrm{upper} \\ $$$$\mathrm{L}_{\mathrm{3}} \:=\:\mathrm{6}\:\mathrm{cm} \\ $$$$\Omega_{\mathrm{3}} \left(\mathrm{1},\mathrm{8}\right) \\ $$$$ \\ $$$$\mathrm{L}\:=\:\mathrm{L}_{\mathrm{1}} +\mathrm{L}_{\mathrm{2}} +\mathrm{L}_{\mathrm{3}} \:=\:\mathrm{8}+\mathrm{4}+\mathrm{6}\:=\:\mathrm{18}\:\mathrm{cm} \\ $$$$ \\ $$$$\mathrm{L}\overset{\rightarrow} {\mathrm{OG}}\:=\:\mathrm{L}_{\mathrm{1}} \overset{\rightarrow} {\mathrm{O}\Omega_{\mathrm{1}} }+\mathrm{L}_{\mathrm{2}} \overset{\rightarrow} {\mathrm{O}\Omega_{\mathrm{2}} }+\mathrm{L}_{\mathrm{3}} \overset{\rightarrow} {\mathrm{O}\Omega_{\mathrm{3}} } \\ $$$$\overset{\rightarrow} {\mathrm{OG}}\:=\:\frac{\mathrm{8}}{\mathrm{18}}\left(\mathrm{0},\mathrm{4}\right)+\frac{\mathrm{4}}{\mathrm{18}}\left(−\mathrm{2},\mathrm{4}\right)+\frac{\mathrm{6}}{\mathrm{18}}\left(\mathrm{1},\mathrm{8}\right) \\ $$$$\mathrm{G}\:=\:\left(−\frac{\mathrm{1}}{\mathrm{9}},\frac{\mathrm{16}}{\mathrm{3}}\right) \\ $$
