Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 150884 by mathdanisur last updated on 16/Aug/21

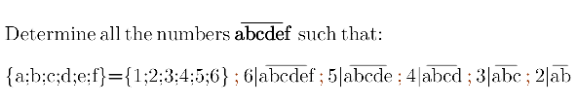
Answered by Rasheed.Sindhi last updated on 16/Aug/21

abcdef^(−) =?;{a,b,c,d,e,f}={1,2,3,4,5,6} 6∣abcdef^(−) ,5∣abcde^(−) ,4∣abcd^(−) ,3∣abc^(−) ,2∣ab^(−) ≪⇆⇄⇆⇄⇆⇄⇆⇄⇆⇄⇆⇄⇆≫ 6∣abcdef⇒3∣abcdef 3∣abcdef ∧ 3∣abc⇒3∣def ^• 3∣abc ∧ 3∣def 5∣abcde⇒e=5 ^• e=5 2∣ab⇒b=2,4,6 ^• b=2,4,6 6∣abcdef⇒f=2,4,6 ^• f=2,4,6 4∣abcd⇒4∣cd⇒d=2,4,6 ^• d=2,4,6 There′re two pieces of the number both divisibleby 3 ⇒ ^• 3∣(a+b+c) ∧ 3∣(d+e+f) Let′s make def piece first: e=5 f & d are even(2,4,6) and d+e+f is multiple of 3: f=2⇒The possible values for def: 452,652 both aren′t multiple of 3 ∴ f≠2 f=4, def=254,654. 3∤254; 3∣654 ∴ 654 is succesful candidate for def f=6,def=256,456. only 456 is multiple of 3 and hence succesful candidate. Let′s make other piece abc: Case1:def=654: ∵ 4∣cd⇒cd=16,36, 56(rejected b/c 5 has been already used) ∴ c=1,3 ∵ b is even and only 2 has been remaine unused from the given set. ∴ b=2 Possible candidates for abc are: 321 & 123 (thanks God, 3 divides both) abcdef=123654,321654 (when def=654) Case1:def=456: d=4⇒c=2,4,6(latter two are already used) ∴c=2 but then there remains no value for b which is also even. ∴ When def=456 there′s no value for abcdef(required number) So finally abcdef=123654,321654

$$\overline {\mathrm{abcdef}}=?;\left\{\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d},\mathrm{e},\mathrm{f}\right\}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6}\right\} \\ $$$$\mathrm{6}\overline {\mid\mathrm{abcdef}},\mathrm{5}\mid\overline {\mathrm{abcde}},\mathrm{4}\mid\overline {\mathrm{abcd}},\mathrm{3}\mid\overline {\mathrm{abc}},\mathrm{2}\mid\overline {\mathrm{ab}} \\ $$$$\ll\leftrightarrows\rightleftarrows\leftrightarrows\rightleftarrows\leftrightarrows\rightleftarrows\leftrightarrows\rightleftarrows\leftrightarrows\rightleftarrows\leftrightarrows\rightleftarrows\leftrightarrows\gg \\ $$$$\mathrm{6}\mid\mathrm{abcdef}\Rightarrow\mathrm{3}\mid\mathrm{abcdef} \\ $$$$\mathrm{3}\mid\mathrm{abcdef}\:\wedge\:\mathrm{3}\mid\mathrm{abc}\Rightarrow\mathrm{3}\mid\mathrm{def} \\ $$$$\:^{\bullet} \:\mathrm{3}\mid\mathrm{abc}\:\wedge\:\mathrm{3}\mid\mathrm{def} \\ $$$$\mathrm{5}\mid\mathrm{abcde}\Rightarrow\mathrm{e}=\mathrm{5} \\ $$$$\:^{\bullet} \mathrm{e}=\mathrm{5} \\ $$$$\mathrm{2}\mid\mathrm{ab}\Rightarrow\mathrm{b}=\mathrm{2},\mathrm{4},\mathrm{6} \\ $$$$\:^{\bullet} \mathrm{b}=\mathrm{2},\mathrm{4},\mathrm{6} \\ $$$$\mathrm{6}\mid\mathrm{abcdef}\Rightarrow\mathrm{f}=\mathrm{2},\mathrm{4},\mathrm{6} \\ $$$$\:^{\bullet} \mathrm{f}=\mathrm{2},\mathrm{4},\mathrm{6} \\ $$$$\mathrm{4}\mid\mathrm{abcd}\Rightarrow\mathrm{4}\mid\mathrm{cd}\Rightarrow\mathrm{d}=\mathrm{2},\mathrm{4},\mathrm{6} \\ $$$$\:^{\bullet} \mathrm{d}=\mathrm{2},\mathrm{4},\mathrm{6} \\ $$$$\mathrm{There}'\mathrm{re}\:\mathrm{two}\:\mathrm{pieces}\:\mathrm{of}\:\mathrm{the}\:\mathrm{number} \\ $$$$\mathrm{both}\:\mathrm{divisibleby}\:\mathrm{3}\:\Rightarrow \\ $$$$\:^{\bullet} \mathrm{3}\mid\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\:\wedge\:\mathrm{3}\mid\left(\mathrm{d}+\mathrm{e}+\mathrm{f}\right) \\ $$$$\underline{\mathrm{Let}'\mathrm{s}\:\mathrm{make}\:\boldsymbol{\mathrm{def}}\:\mathrm{piece}\:\mathrm{first}:} \\ $$$$\mathrm{e}=\mathrm{5}\:\mathrm{f}\:\&\:\mathrm{d}\:\mathrm{are}\:\mathrm{even}\left(\mathrm{2},\mathrm{4},\mathrm{6}\right)\:\mathrm{and}\:\mathrm{d}+\mathrm{e}+\mathrm{f} \\ $$$$\mathrm{is}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{3}: \\ $$$$\mathrm{f}=\mathrm{2}\Rightarrow\mathrm{The}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{def}: \\ $$$$\mathrm{452},\mathrm{652}\:\mathrm{both}\:\mathrm{aren}'\mathrm{t}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{3} \\ $$$$\therefore\:\mathrm{f}\neq\mathrm{2} \\ $$$$\mathrm{f}=\mathrm{4},\:\mathrm{def}=\mathrm{254},\mathrm{654}.\:\mathrm{3}\nmid\mathrm{254};\:\mathrm{3}\mid\mathrm{654} \\ $$$$\therefore\:\mathrm{654}\:\mathrm{is}\:\mathrm{succesful}\:\mathrm{candidate}\:\mathrm{for}\:\mathrm{def} \\ $$$$\mathrm{f}=\mathrm{6},\mathrm{def}=\mathrm{256},\mathrm{456}.\:\mathrm{only}\:\mathrm{456}\:\mathrm{is}\:\mathrm{multiple}\: \\ $$$$\mathrm{of}\:\mathrm{3}\:\mathrm{and}\:\mathrm{hence}\:\mathrm{succesful}\:\mathrm{candidate}. \\ $$$$\underline{\mathrm{Let}'\mathrm{s}\:\mathrm{make}\:\mathrm{other}\:\mathrm{piece}\:\boldsymbol{\mathrm{abc}}:} \\ $$$$\:\mathrm{Case1}:\underline{\mathrm{def}=\mathrm{654}:}\:\because\:\mathrm{4}\mid\mathrm{cd}\Rightarrow\mathrm{cd}=\mathrm{16},\mathrm{36}, \\ $$$$\mathrm{56}\left({rejected}\:{b}/{c}\:\mathrm{5}\:{has}\:{been}\:{already}\right. \\ $$$$\left.{used}\right) \\ $$$$\therefore\:\mathrm{c}=\mathrm{1},\mathrm{3} \\ $$$$\because\:\mathrm{b}\:\mathrm{is}\:\mathrm{even}\:\mathrm{and}\:\mathrm{only}\:\mathrm{2}\:\mathrm{has}\:\mathrm{been}\: \\ $$$$\mathrm{remaine}\:\mathrm{unused}\:\mathrm{from}\:\mathrm{the}\:\mathrm{given}\:\mathrm{set}. \\ $$$$\therefore\:\mathrm{b}=\mathrm{2} \\ $$$$\mathrm{Possible}\:\mathrm{candidates}\:\mathrm{for}\:\mathrm{abc}\:\mathrm{are}: \\ $$$$\mathrm{321}\:\&\:\mathrm{123}\:\left(\mathrm{thanks}\:\mathrm{God},\:\mathrm{3}\:\mathrm{divides}\:\mathrm{both}\right) \\ $$$$\mathrm{abcdef}=\mathrm{123654},\mathrm{321654}\:\left(\mathrm{when}\:\mathrm{def}=\mathrm{654}\right) \\ $$$$\:\mathrm{Case1}:\underline{\mathrm{def}=\mathrm{456}:}\:\mathrm{d}=\mathrm{4}\Rightarrow\mathrm{c}=\mathrm{2},\mathrm{4},\mathrm{6}\left({latter}\right. \\ $$$$\left.{two}\:{are}\:{already}\:{used}\right) \\ $$$$\therefore\mathrm{c}=\mathrm{2}\:\mathrm{but}\:\mathrm{then}\:\mathrm{there}\:\mathrm{remains}\:\mathrm{no} \\ $$$$\mathrm{value}\:\mathrm{for}\:\mathrm{b}\:\mathrm{which}\:\mathrm{is}\:\mathrm{also}\:\mathrm{even}. \\ $$$$\therefore\:\mathrm{When}\:\mathrm{def}=\mathrm{456}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{value} \\ $$$$\mathrm{for}\:\mathrm{abcdef}\left(\mathrm{required}\:\mathrm{number}\right) \\ $$$$\:\:\:\:\:\:\mathrm{So}\:\mathrm{finally} \\ $$$$\:\:\:\:\:\mathrm{abcdef}=\mathrm{123654},\mathrm{321654} \\ $$

Commented by mathdanisur last updated on 16/Aug/21

Nice Ser, thank you

$$\mathrm{Nice}\:\mathrm{Ser},\:\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com