Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 150305 by Tawa11 last updated on 10/Aug/21

Commented by Tawa11 last updated on 10/Aug/21

Find (R/r)

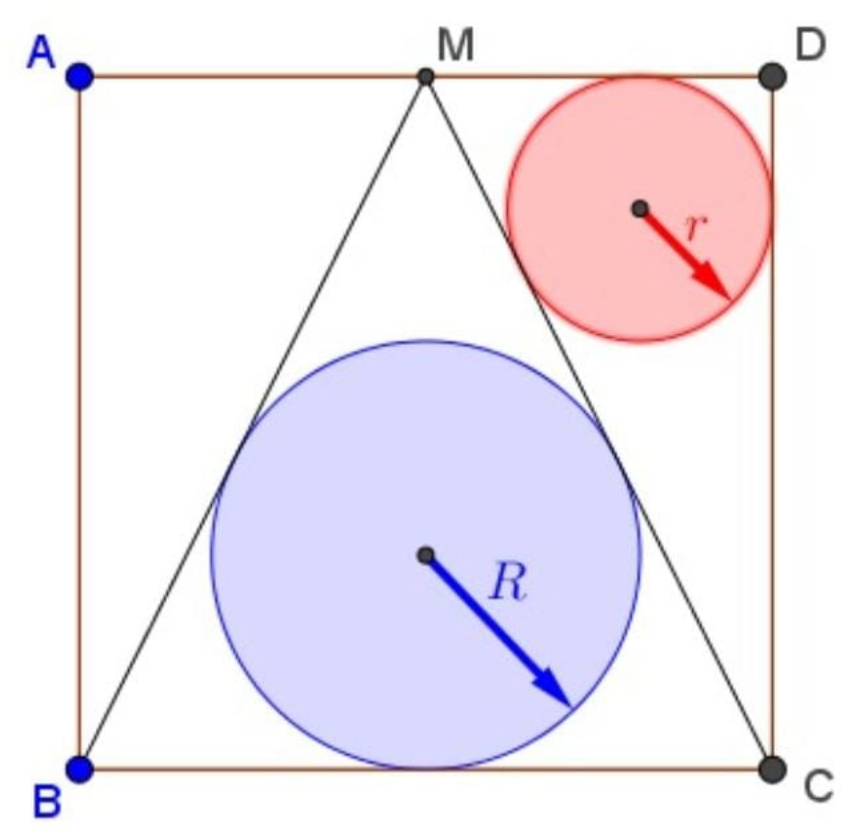
$$\mathrm{Find}\:\:\:\:\frac{\mathrm{R}}{\mathrm{r}} \\ $$

Answered by nimnim last updated on 11/Aug/21

With midpoint M ar(△MBC)=2×ar(△MDC) AB=2a (say) BM=CM=(√((2a)^2 +a^2 ))=a(√5) In △MBC, s=((a(√5)+a(√5)+2a)/2)=((√5)+1)a R=((ar(△MBC))/(((√5)+1)a)) In △MDC, s=((a(√5)+a+2a)/2)=((((√5)+3)a)/2) r=((ar(△MDC))/(((√5)+3)a/2))=((2×ar(△MDC))/( ((√5)+3)a)) ∴ (R/r)=((ar(△MBC))/(((√5)+1)a))×((((√5)+3)a)/(2×ar(△MDC))) =(((√5)+3)/( (√5)+1))★ or =(((√5)+3)/( (√5)+1))×(((√5)−1)/( (√5)−1)) =((5+3(√5)−(√5)−3)/4) =((1+(√5))/2)= ϕ (golden ratio)

$${With}\:{midpoint}\:{M} \\ $$$${ar}\left(\bigtriangleup{MBC}\right)=\mathrm{2}×{ar}\left(\bigtriangleup{MDC}\right) \\ $$$${AB}=\mathrm{2}{a}\:\left({say}\right) \\ $$$${BM}={CM}=\sqrt{\left(\mathrm{2}{a}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} }={a}\sqrt{\mathrm{5}} \\ $$$${In}\:\bigtriangleup{MBC},\:{s}=\frac{{a}\sqrt{\mathrm{5}}+{a}\sqrt{\mathrm{5}}+\mathrm{2}{a}}{\mathrm{2}}=\left(\sqrt{\mathrm{5}}+\mathrm{1}\right){a} \\ $$$${R}=\frac{{ar}\left(\bigtriangleup{MBC}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right){a}} \\ $$$${In}\:\bigtriangleup{MDC},\:{s}=\frac{{a}\sqrt{\mathrm{5}}+{a}+\mathrm{2}{a}}{\mathrm{2}}=\frac{\left(\sqrt{\mathrm{5}}+\mathrm{3}\right){a}}{\mathrm{2}} \\ $$$${r}=\frac{{ar}\left(\bigtriangleup{MDC}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{3}\right){a}/\mathrm{2}}=\frac{\mathrm{2}×{ar}\left(\bigtriangleup{MDC}\right)}{\:\left(\sqrt{\mathrm{5}}+\mathrm{3}\right){a}} \\ $$$$\therefore\:\frac{{R}}{{r}}=\frac{{ar}\left(\bigtriangleup{MBC}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right){a}}×\frac{\left(\sqrt{\mathrm{5}}+\mathrm{3}\right){a}}{\mathrm{2}×{ar}\left(\bigtriangleup{MDC}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{5}}+\mathrm{3}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}\bigstar \\ $$$$\:\:{or}\:\:\:=\frac{\sqrt{\mathrm{5}}+\mathrm{3}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}×\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{5}}−\sqrt{\mathrm{5}}−\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}=\:\varphi\:\left({golden}\:{ratio}\right) \\ $$

Commented by Tawa11 last updated on 11/Aug/21

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com