
Previous in Relation and Functions Next in Relation and Functions
Question Number 149551 by puissant last updated on 06/Aug/21
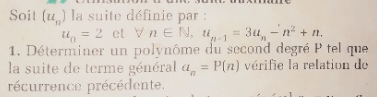
Answered by Olaf_Thorendsen last updated on 06/Aug/21
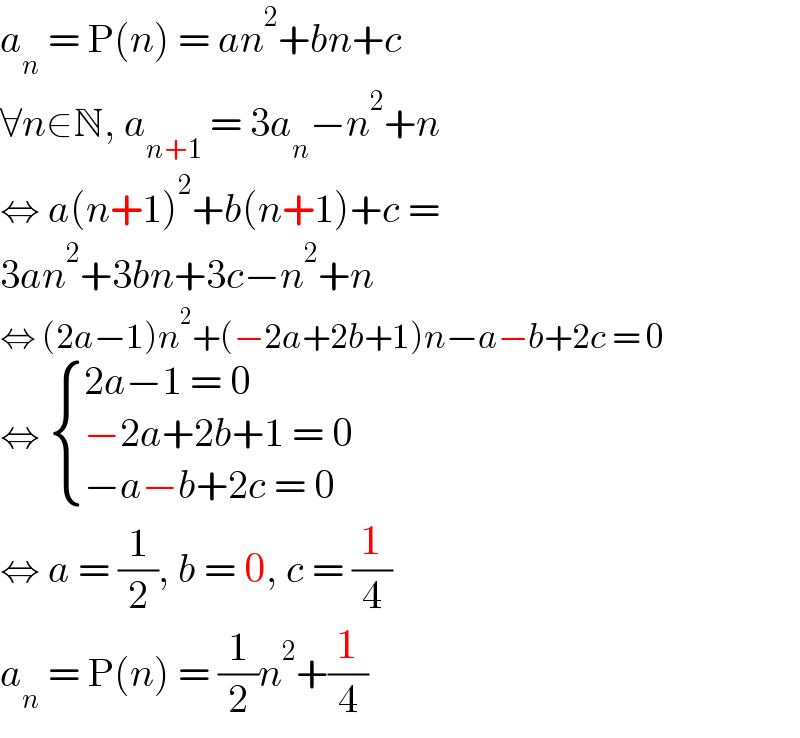
$${a}_{{n}} \:=\:\mathrm{P}\left({n}\right)\:=\:{an}^{\mathrm{2}} +{bn}+{c} \\ $$$$\forall{n}\in\mathbb{N},\:{a}_{{n}+\mathrm{1}} \:=\:\mathrm{3}{a}_{{n}} −{n}^{\mathrm{2}} +{n} \\ $$$$\Leftrightarrow\:{a}\left({n}+\mathrm{1}\right)^{\mathrm{2}} +{b}\left({n}+\mathrm{1}\right)+{c}\:= \\ $$$$\mathrm{3}{an}^{\mathrm{2}} +\mathrm{3}{bn}+\mathrm{3}{c}−{n}^{\mathrm{2}} +{n} \\ $$$$\Leftrightarrow\:\left(\mathrm{2}{a}−\mathrm{1}\right){n}^{\mathrm{2}} +\left(−\mathrm{2}{a}+\mathrm{2}{b}+\mathrm{1}\right){n}−{a}−{b}+\mathrm{2}{c}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\begin{cases}{\mathrm{2}{a}−\mathrm{1}\:=\:\mathrm{0}}\\{−\mathrm{2}{a}+\mathrm{2}{b}+\mathrm{1}\:=\:\mathrm{0}}\\{−{a}−{b}+\mathrm{2}{c}\:=\:\mathrm{0}}\end{cases} \\ $$$$\Leftrightarrow\:{a}\:=\:\frac{\mathrm{1}}{\mathrm{2}},\:{b}\:=\:\mathrm{0},\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${a}_{{n}} \:=\:\mathrm{P}\left({n}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by puissant last updated on 06/Aug/21
$$\mathrm{merci}\:\mathrm{monsieur}\:\mathrm{Olaf}... \\ $$
Commented by puissant last updated on 06/Aug/21
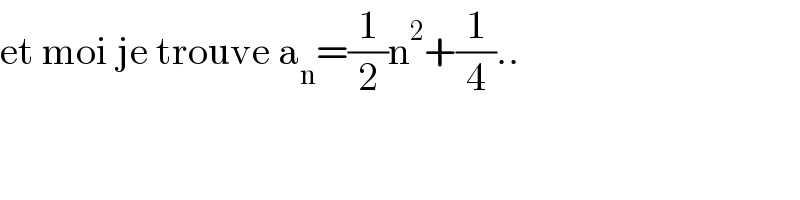
$$\mathrm{et}\:\mathrm{moi}\:\mathrm{je}\:\mathrm{trouve}\:\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{n}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}.. \\ $$
Commented by Olaf_Thorendsen last updated on 06/Aug/21

$$\mathrm{j}'\mathrm{ai}\:\mathrm{rectifie} \\ $$
Commented by puissant last updated on 06/Aug/21

$$\mathrm{merci}.. \\ $$
