
Question Number 149219 by mathdanisur last updated on 03/Aug/21
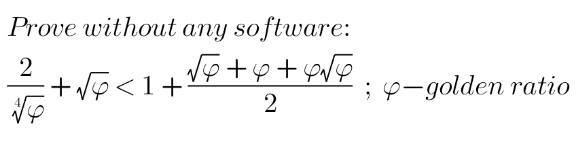
Answered by mindispower last updated on 03/Aug/21
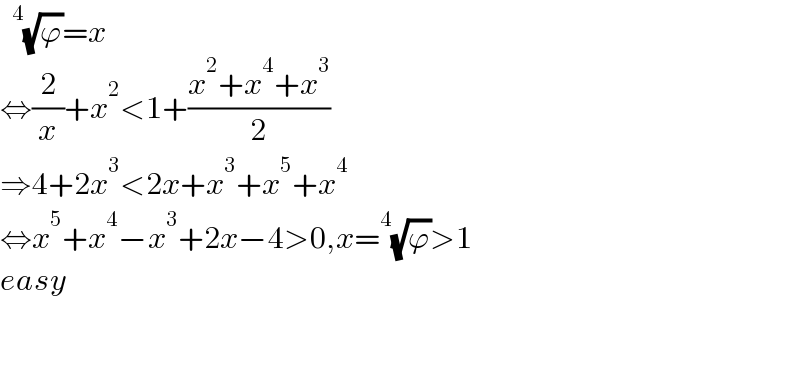
$$\:\:^{\mathrm{4}} \sqrt{\varphi}={x} \\ $$$$\Leftrightarrow\frac{\mathrm{2}}{{x}}+{x}^{\mathrm{2}} <\mathrm{1}+\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}+\mathrm{2}{x}^{\mathrm{3}} <\mathrm{2}{x}+{x}^{\mathrm{3}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} \\ $$$$\Leftrightarrow{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +\mathrm{2}{x}−\mathrm{4}>\mathrm{0},{x}=^{\mathrm{4}} \sqrt{\varphi}>\mathrm{1} \\ $$$${easy} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 03/Aug/21
$${Thank}\:{You}\:{Ser}\:{thats}\:{it}... \\ $$
Answered by dumitrel last updated on 03/Aug/21
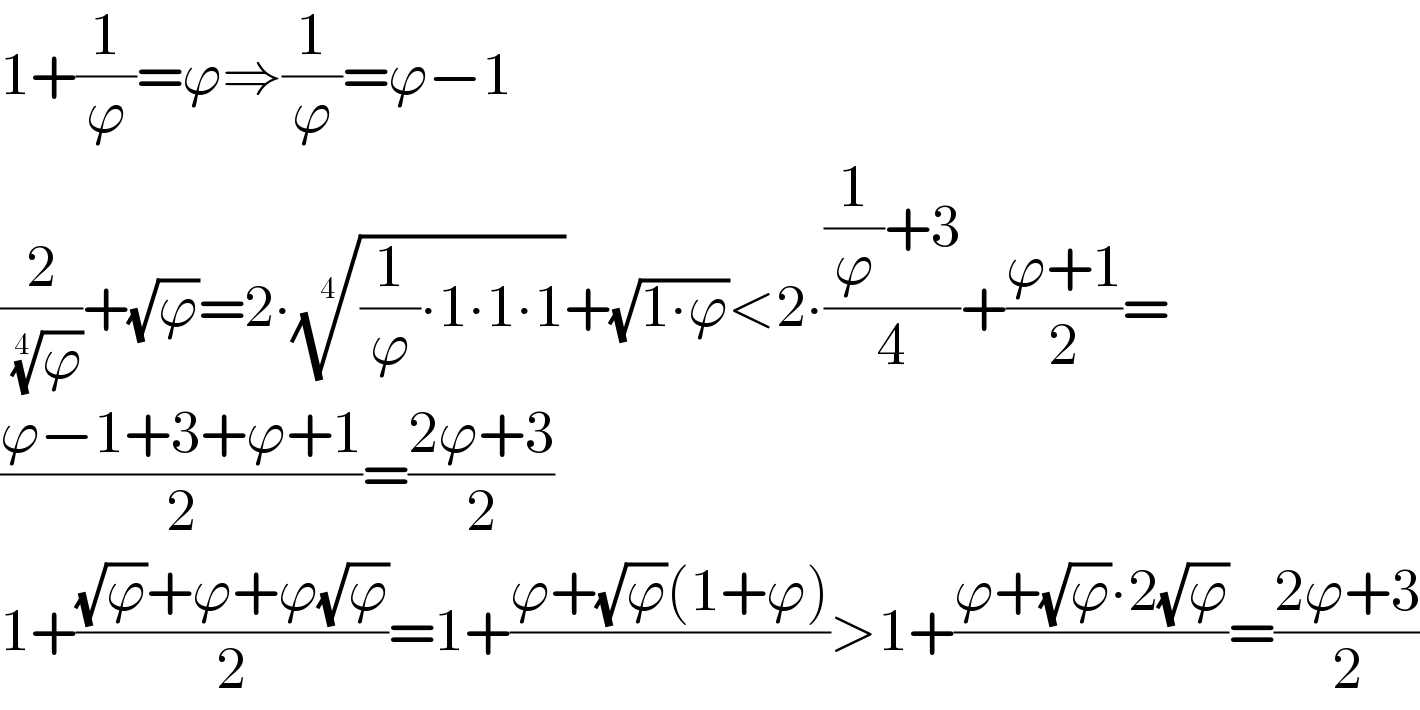
$$\mathrm{1}+\frac{\mathrm{1}}{\varphi}=\varphi\Rightarrow\frac{\mathrm{1}}{\varphi}=\varphi−\mathrm{1} \\ $$$$\frac{\mathrm{2}}{\:\sqrt[{\mathrm{4}}]{\varphi}}+\sqrt{\varphi}=\mathrm{2}\centerdot\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}}{\varphi}\centerdot\mathrm{1}\centerdot\mathrm{1}\centerdot\mathrm{1}}+\sqrt{\mathrm{1}\centerdot\varphi}<\mathrm{2}\centerdot\frac{\frac{\mathrm{1}}{\varphi}+\mathrm{3}}{\mathrm{4}}+\frac{\varphi+\mathrm{1}}{\mathrm{2}}= \\ $$$$\frac{\varphi−\mathrm{1}+\mathrm{3}+\varphi+\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}\varphi+\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\sqrt{\varphi}+\varphi+\varphi\sqrt{\varphi}}{\mathrm{2}}=\mathrm{1}+\frac{\varphi+\sqrt{\varphi}\left(\mathrm{1}+\varphi\right)}{}>\mathrm{1}+\frac{\varphi+\sqrt{\varphi}\centerdot\mathrm{2}\sqrt{\varphi}}{}=\frac{\mathrm{2}\varphi+\mathrm{3}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Ser},\:{Thank}\:{You} \\ $$
