Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 147585 by mathdanisur last updated on 22/Jul/21

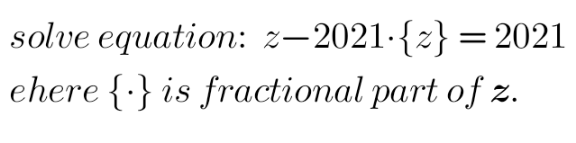
Answered by Rasheed.Sindhi last updated on 22/Jul/21

z=w+f : whole number & fraction<1 w+f−2021f=2021 w=2021f−f+2021 w=2020f+2021 Let f=(p/q) ; p & q coprime p<q w=2020((p/q))+2021 z=w+f=2020((p/q))+2021+(p/q) z=2021((p/q))+2021 z=2021(((p+q)/q)) q ∣ 2020 q=2⇒p=1⇒f=(1/2)⇒w=2020((1/2))+2021 w=3031⇒z=3031(1/2) q=4⇒p=1,3⇒f=(1/4),(3/4)⇒w=2020((1/4))+2021 w=2526⇒z=2526(1/4) w=2020((3/4))+2021=3536⇒z=3536(3/4) q=5⇒p=1,2,3,4⇒f=(1/5),(2/5),(3/5),(4/5) w=2020((1/5))+2021=2425 z=2425(1/5) z=2021(((p+q)/q)) Where q ∣ 2020 ∧ (p,q)=1 ∧ p<q

$$\:\:\:{z}={w}+{f}\::\:{whole}\:{number}\:\&\:{fraction}<\mathrm{1} \\ $$$$\:\:\:\:{w}+{f}−\mathrm{2021}{f}=\mathrm{2021} \\ $$$$\:\:\:\:{w}=\mathrm{2021}{f}−{f}+\mathrm{2021} \\ $$$$\:\:\:\:{w}=\mathrm{2020}{f}+\mathrm{2021} \\ $$$${Let}\:{f}=\frac{{p}}{{q}}\:;\:{p}\:\&\:{q}\:{coprime}\:{p}<{q} \\ $$$$\:\:\:\:{w}=\mathrm{2020}\left(\frac{{p}}{{q}}\right)+\mathrm{2021} \\ $$$$\:\:\:{z}={w}+{f}=\mathrm{2020}\left(\frac{{p}}{{q}}\right)+\mathrm{2021}+\frac{{p}}{{q}} \\ $$$$\:\:\:{z}=\mathrm{2021}\left(\frac{{p}}{{q}}\right)+\mathrm{2021} \\ $$$$\:\:\:{z}=\mathrm{2021}\left(\frac{{p}+{q}}{{q}}\right) \\ $$$${q}\:\mid\:\mathrm{2020}\: \\ $$$${q}=\mathrm{2}\Rightarrow{p}=\mathrm{1}\Rightarrow{f}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{w}=\mathrm{2020}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2021} \\ $$$${w}=\mathrm{3031}\Rightarrow{z}=\mathrm{3031}\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$${q}=\mathrm{4}\Rightarrow{p}=\mathrm{1},\mathrm{3}\Rightarrow{f}=\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{3}}{\mathrm{4}}\Rightarrow{w}=\mathrm{2020}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{2021} \\ $$$${w}=\mathrm{2526}\Rightarrow{z}=\mathrm{2526}\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${w}=\mathrm{2020}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)+\mathrm{2021}=\mathrm{3536}\Rightarrow{z}=\mathrm{3536}\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${q}=\mathrm{5}\Rightarrow{p}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\Rightarrow{f}=\frac{\mathrm{1}}{\mathrm{5}},\frac{\mathrm{2}}{\mathrm{5}},\frac{\mathrm{3}}{\mathrm{5}},\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${w}=\mathrm{2020}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)+\mathrm{2021}=\mathrm{2425} \\ $$$${z}=\mathrm{2425}\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{z}=\mathrm{2021}\left(\frac{{p}+{q}}{{q}}\right) \\ $$$$\:{Where}\:\:{q}\:\mid\:\mathrm{2020}\:\wedge\:\left({p},{q}\right)=\mathrm{1}\:\wedge\:{p}<{q} \\ $$

Commented by mathdanisur last updated on 22/Jul/21

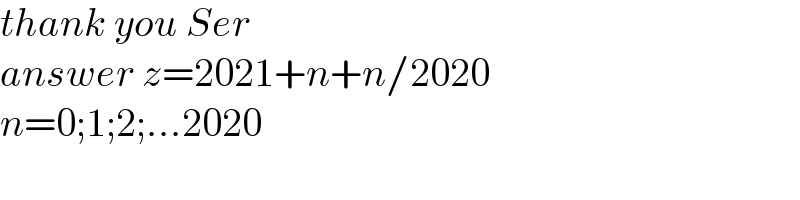
thank you Ser answer z=2021+n+n/2020 n=0;1;2;...2020

$${thank}\:{you}\:{Ser} \\ $$$${answer}\:{z}=\mathrm{2021}+{n}+{n}/\mathrm{2020} \\ $$$${n}=\mathrm{0};\mathrm{1};\mathrm{2};...\mathrm{2020} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com