
Question Number 147561 by vvvv last updated on 21/Jul/21
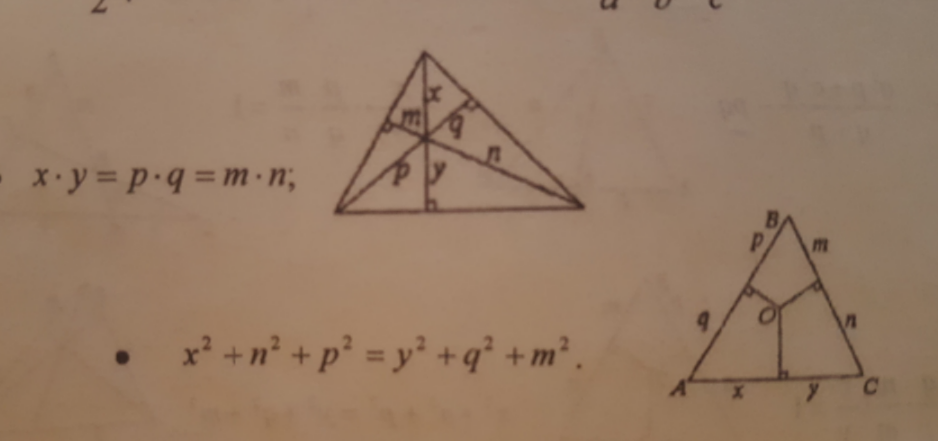
Commented by vvvv last updated on 21/Jul/21

$$\boldsymbol{{prove}} \\ $$
Answered by mr W last updated on 21/Jul/21
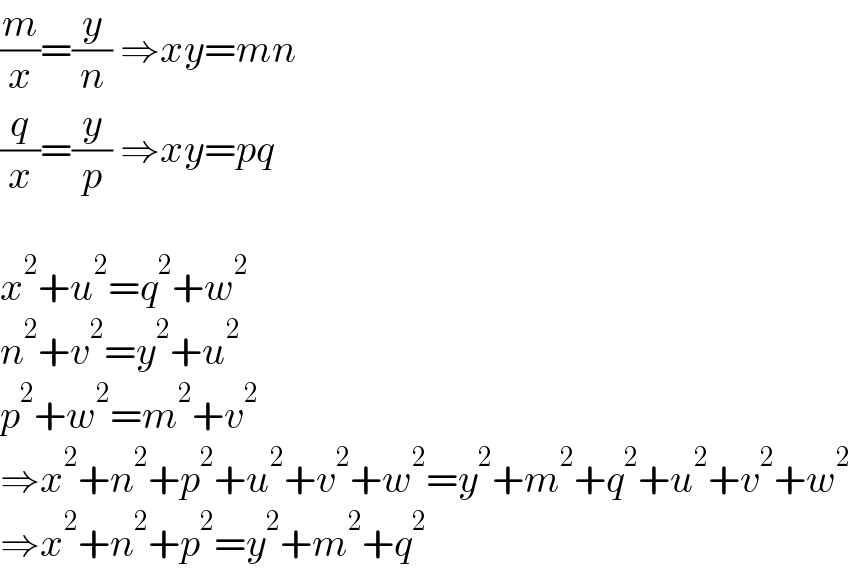
$$\frac{{m}}{{x}}=\frac{{y}}{{n}}\:\Rightarrow{xy}={mn} \\ $$$$\frac{{q}}{{x}}=\frac{{y}}{{p}}\:\Rightarrow{xy}={pq} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{u}^{\mathrm{2}} ={q}^{\mathrm{2}} +{w}^{\mathrm{2}} \\ $$$${n}^{\mathrm{2}} +{v}^{\mathrm{2}} ={y}^{\mathrm{2}} +{u}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} +{w}^{\mathrm{2}} ={m}^{\mathrm{2}} +{v}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{n}^{\mathrm{2}} +{p}^{\mathrm{2}} +{u}^{\mathrm{2}} +{v}^{\mathrm{2}} +{w}^{\mathrm{2}} ={y}^{\mathrm{2}} +{m}^{\mathrm{2}} +{q}^{\mathrm{2}} +{u}^{\mathrm{2}} +{v}^{\mathrm{2}} +{w}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{n}^{\mathrm{2}} +{p}^{\mathrm{2}} ={y}^{\mathrm{2}} +{m}^{\mathrm{2}} +{q}^{\mathrm{2}} \\ $$
Commented by vvvv last updated on 22/Jul/21

$$\boldsymbol{{u}}=?\:\:\boldsymbol{{w}}=?\:\:\boldsymbol{{v}}=?\:\:.....? \\ $$
Commented by mr W last updated on 22/Jul/21
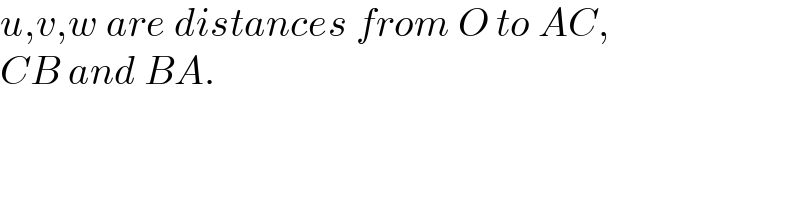
$${u},{v},{w}\:{are}\:{distances}\:{from}\:{O}\:{to}\:{AC},\: \\ $$$${CB}\:{and}\:{BA}. \\ $$
