
Question Number 147272 by mathdanisur last updated on 19/Jul/21
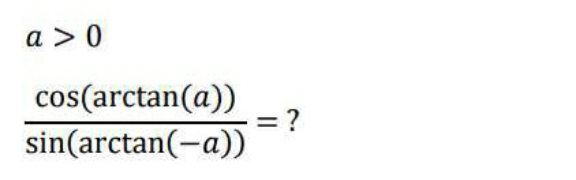
Answered by puissant last updated on 19/Jul/21

$${y}={arctan}\left({a}\right)\:\Rightarrow\:{cos}\left({arctan}\left({a}\right)\right)={cos}\left({y}\right) \\ $$$$\mathrm{1}+{tan}^{\mathrm{2}} {y}=\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {y}}\:\Rightarrow\:{cos}^{\mathrm{2}} {y}=\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {y}} \\ $$$$\Rightarrow{cos}^{\mathrm{2}} \left({arctan}\left({a}\right)\right)=\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} \left({arctan}\left({a}\right)\right)}=\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{cos}\left({arctan}\left({a}\right)\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$$...\:\:\:{sin}^{\mathrm{2}} \left({arctan}\left(−{a}\right)\right)=\mathrm{1}−{cos}^{\mathrm{2}} \left({arctan}\left(−{a}\right)\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\left(−{a}\right)^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} }=\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{sin}\left({arctan}\left(−{a}\right)\right)=\frac{\mid{a}\mid}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$${a}>\mathrm{0}\:\Rightarrow\:{sin}\left({arctan}\left(−{a}\right)\right)=\frac{{a}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$$\:\:\frac{{cos}\left({arctan}\left({a}\right)\right)}{{sin}\left({arctan}\left(−{a}\right)\right)}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}×\frac{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}}=\frac{\mathrm{1}}{{a}}.... \\ $$
Commented by nadovic last updated on 19/Jul/21

$${Nice}\:{one} \\ $$
Commented by mathdanisur last updated on 19/Jul/21
$${thank}\:{you}\:{Sir}\:{cool} \\ $$
Commented by puissant last updated on 03/Sep/21

$${Q}\mathrm{863} \\ $$
