Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 147091 by aliibrahim1 last updated on 17/Jul/21

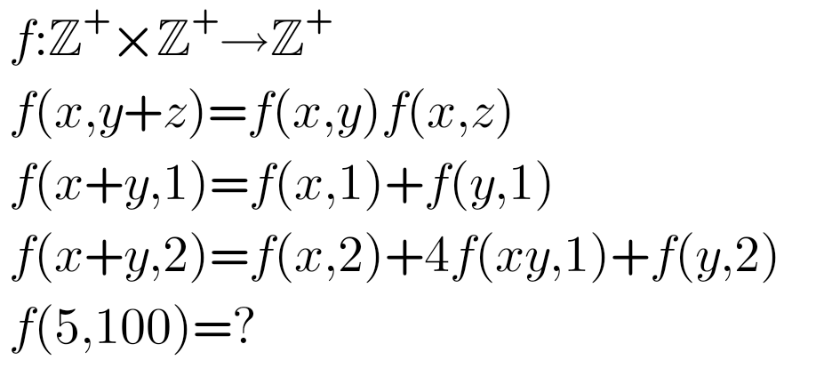
Answered by Olaf_Thorendsen last updated on 18/Jul/21

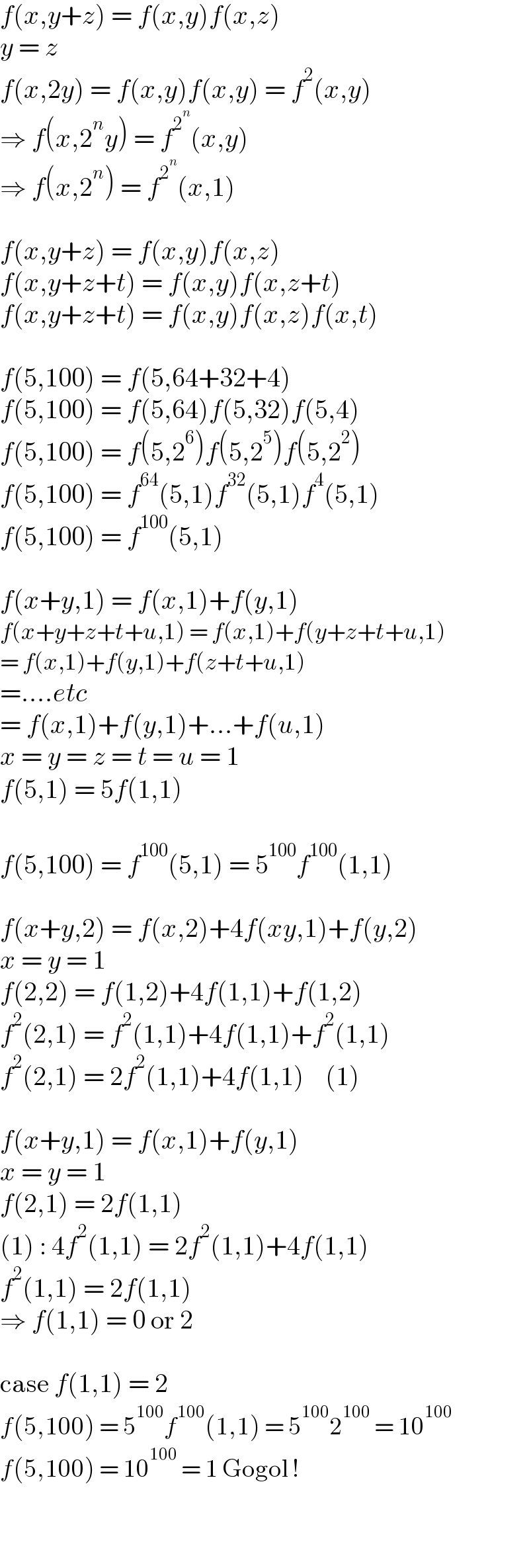
f(x,y+z) = f(x,y)f(x,z) y = z f(x,2y) = f(x,y)f(x,y) = f^2 (x,y) ⇒ f(x,2^n y) = f^2^n (x,y) ⇒ f(x,2^n ) = f^2^n (x,1) f(x,y+z) = f(x,y)f(x,z) f(x,y+z+t) = f(x,y)f(x,z+t) f(x,y+z+t) = f(x,y)f(x,z)f(x,t) f(5,100) = f(5,64+32+4) f(5,100) = f(5,64)f(5,32)f(5,4) f(5,100) = f(5,2^6 )f(5,2^5 )f(5,2^2 ) f(5,100) = f^(64) (5,1)f^(32) (5,1)f^4 (5,1) f(5,100) = f^(100) (5,1) f(x+y,1) = f(x,1)+f(y,1) f(x+y+z+t+u,1) = f(x,1)+f(y+z+t+u,1) = f(x,1)+f(y,1)+f(z+t+u,1) =....etc = f(x,1)+f(y,1)+...+f(u,1) x = y = z = t = u = 1 f(5,1) = 5f(1,1) f(5,100) = f^(100) (5,1) = 5^(100) f^(100) (1,1) f(x+y,2) = f(x,2)+4f(xy,1)+f(y,2) x = y = 1 f(2,2) = f(1,2)+4f(1,1)+f(1,2) f^2 (2,1) = f^2 (1,1)+4f(1,1)+f^2 (1,1) f^2 (2,1) = 2f^2 (1,1)+4f(1,1) (1) f(x+y,1) = f(x,1)+f(y,1) x = y = 1 f(2,1) = 2f(1,1) (1) : 4f^2 (1,1) = 2f^2 (1,1)+4f(1,1) f^2 (1,1) = 2f(1,1) ⇒ f(1,1) = 0 or 2 case f(1,1) = 2 f(5,100) = 5^(100) f^(100) (1,1) = 5^(100) 2^(100) = 10^(100) f(5,100) = 10^(100) = 1 Gogol !

$${f}\left({x},{y}+{z}\right)\:=\:{f}\left({x},{y}\right){f}\left({x},{z}\right) \\ $$$${y}\:=\:{z} \\ $$$${f}\left({x},\mathrm{2}{y}\right)\:=\:{f}\left({x},{y}\right){f}\left({x},{y}\right)\:=\:{f}^{\mathrm{2}} \left({x},{y}\right) \\ $$$$\Rightarrow\:{f}\left({x},\mathrm{2}^{{n}} {y}\right)\:=\:{f}^{\mathrm{2}^{{n}} } \left({x},{y}\right) \\ $$$$\Rightarrow\:{f}\left({x},\mathrm{2}^{{n}} \right)\:=\:{f}^{\mathrm{2}^{{n}} } \left({x},\mathrm{1}\right) \\ $$$$ \\ $$$${f}\left({x},{y}+{z}\right)\:=\:{f}\left({x},{y}\right){f}\left({x},{z}\right) \\ $$$${f}\left({x},{y}+{z}+{t}\right)\:=\:{f}\left({x},{y}\right){f}\left({x},{z}+{t}\right) \\ $$$${f}\left({x},{y}+{z}+{t}\right)\:=\:{f}\left({x},{y}\right){f}\left({x},{z}\right){f}\left({x},{t}\right) \\ $$$$ \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:{f}\left(\mathrm{5},\mathrm{64}+\mathrm{32}+\mathrm{4}\right) \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:{f}\left(\mathrm{5},\mathrm{64}\right){f}\left(\mathrm{5},\mathrm{32}\right){f}\left(\mathrm{5},\mathrm{4}\right) \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:{f}\left(\mathrm{5},\mathrm{2}^{\mathrm{6}} \right){f}\left(\mathrm{5},\mathrm{2}^{\mathrm{5}} \right){f}\left(\mathrm{5},\mathrm{2}^{\mathrm{2}} \right) \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:{f}^{\mathrm{64}} \left(\mathrm{5},\mathrm{1}\right){f}^{\mathrm{32}} \left(\mathrm{5},\mathrm{1}\right){f}^{\mathrm{4}} \left(\mathrm{5},\mathrm{1}\right) \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:{f}^{\mathrm{100}} \left(\mathrm{5},\mathrm{1}\right) \\ $$$$ \\ $$$${f}\left({x}+{y},\mathrm{1}\right)\:=\:{f}\left({x},\mathrm{1}\right)+{f}\left({y},\mathrm{1}\right) \\ $$$${f}\left({x}+{y}+{z}+{t}+{u},\mathrm{1}\right)\:=\:{f}\left({x},\mathrm{1}\right)+{f}\left({y}+{z}+{t}+{u},\mathrm{1}\right) \\ $$$$=\:{f}\left({x},\mathrm{1}\right)+{f}\left({y},\mathrm{1}\right)+{f}\left({z}+{t}+{u},\mathrm{1}\right) \\ $$$$=....{etc} \\ $$$$=\:{f}\left({x},\mathrm{1}\right)+{f}\left({y},\mathrm{1}\right)+...+{f}\left({u},\mathrm{1}\right) \\ $$$${x}\:=\:{y}\:=\:{z}\:=\:{t}\:=\:{u}\:=\:\mathrm{1} \\ $$$${f}\left(\mathrm{5},\mathrm{1}\right)\:=\:\mathrm{5}{f}\left(\mathrm{1},\mathrm{1}\right) \\ $$$$ \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:{f}^{\mathrm{100}} \left(\mathrm{5},\mathrm{1}\right)\:=\:\mathrm{5}^{\mathrm{100}} {f}^{\mathrm{100}} \left(\mathrm{1},\mathrm{1}\right) \\ $$$$ \\ $$$${f}\left({x}+{y},\mathrm{2}\right)\:=\:{f}\left({x},\mathrm{2}\right)+\mathrm{4}{f}\left({xy},\mathrm{1}\right)+{f}\left({y},\mathrm{2}\right) \\ $$$${x}\:=\:{y}\:=\:\mathrm{1} \\ $$$${f}\left(\mathrm{2},\mathrm{2}\right)\:=\:{f}\left(\mathrm{1},\mathrm{2}\right)+\mathrm{4}{f}\left(\mathrm{1},\mathrm{1}\right)+{f}\left(\mathrm{1},\mathrm{2}\right) \\ $$$${f}^{\mathrm{2}} \left(\mathrm{2},\mathrm{1}\right)\:=\:{f}^{\mathrm{2}} \left(\mathrm{1},\mathrm{1}\right)+\mathrm{4}{f}\left(\mathrm{1},\mathrm{1}\right)+{f}^{\mathrm{2}} \left(\mathrm{1},\mathrm{1}\right) \\ $$$${f}^{\mathrm{2}} \left(\mathrm{2},\mathrm{1}\right)\:=\:\mathrm{2}{f}^{\mathrm{2}} \left(\mathrm{1},\mathrm{1}\right)+\mathrm{4}{f}\left(\mathrm{1},\mathrm{1}\right)\:\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$${f}\left({x}+{y},\mathrm{1}\right)\:=\:{f}\left({x},\mathrm{1}\right)+{f}\left({y},\mathrm{1}\right) \\ $$$${x}\:=\:{y}\:=\:\mathrm{1} \\ $$$${f}\left(\mathrm{2},\mathrm{1}\right)\:=\:\mathrm{2}{f}\left(\mathrm{1},\mathrm{1}\right) \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{4}{f}^{\mathrm{2}} \left(\mathrm{1},\mathrm{1}\right)\:=\:\mathrm{2}{f}^{\mathrm{2}} \left(\mathrm{1},\mathrm{1}\right)+\mathrm{4}{f}\left(\mathrm{1},\mathrm{1}\right) \\ $$$${f}^{\mathrm{2}} \left(\mathrm{1},\mathrm{1}\right)\:=\:\mathrm{2}{f}\left(\mathrm{1},\mathrm{1}\right) \\ $$$$\Rightarrow\:{f}\left(\mathrm{1},\mathrm{1}\right)\:=\:\mathrm{0}\:\mathrm{or}\:\mathrm{2} \\ $$$$ \\ $$$$\mathrm{case}\:{f}\left(\mathrm{1},\mathrm{1}\right)\:=\:\mathrm{2} \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:\mathrm{5}^{\mathrm{100}} {f}^{\mathrm{100}} \left(\mathrm{1},\mathrm{1}\right)\:=\:\mathrm{5}^{\mathrm{100}} \mathrm{2}^{\mathrm{100}} \:=\:\mathrm{10}^{\mathrm{100}} \\ $$$${f}\left(\mathrm{5},\mathrm{100}\right)\:=\:\mathrm{10}^{\mathrm{100}} \:=\:\mathrm{1}\:\mathrm{Gogol}\:! \\ $$$$ \\ $$

Commented by aliibrahim1 last updated on 18/Jul/21

thank you soo much sir

$${thank}\:{you}\:{soo}\:{much}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com