Question Number 146303 by ajfour last updated on 12/Jul/21
Commented by ajfour last updated on 12/Jul/21

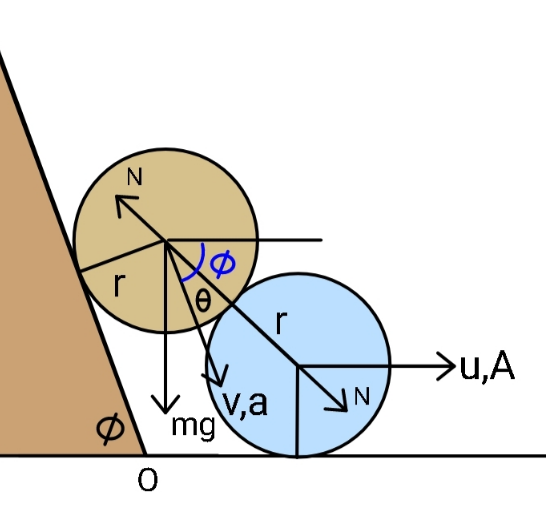
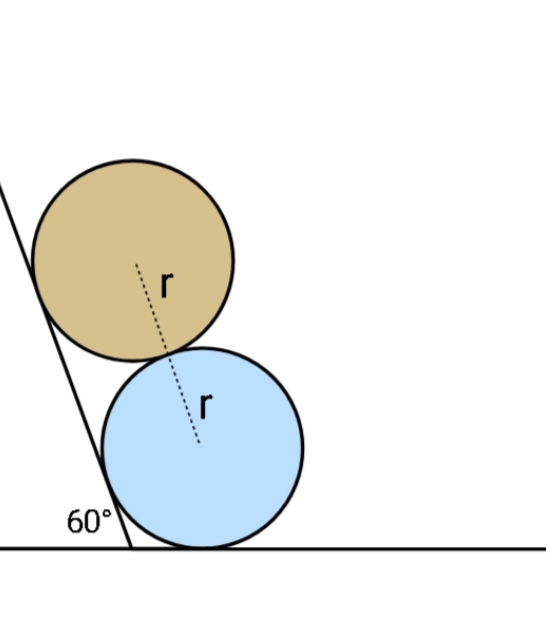
$${If}\:{released}\:{as}\:{shown},\:{and} \\ $$$${assuming}\:{no}\:{friction},\:{find} \\ $$$${after}\:{what}\:{time}\:{does}\:{the}\: \\ $$$${upper}\:{ball}\:{hit}\:{the}\:{ground}? \\ $$
Commented by ajfour last updated on 13/Jul/21

$${just}\:{saw}\:{a}\:{notification}\:{to}\:{this} \\ $$$${question},\:{but}\:{nothing}\:{in}\:{here}.. \\ $$
Commented by Tinku Tara last updated on 13/Jul/21
$$\mathrm{Maybe}\:\mathrm{somebody}\:\mathrm{added}\:\mathrm{something} \\ $$$$\mathrm{and}\:\mathrm{then}\:\mathrm{deleted} \\ $$
Commented by mr W last updated on 13/Jul/21
$${i}\:{added}\:{an}\:{image}\:{comment}\:{and}\:{then}\: \\ $$$${deleted}. \\ $$
Answered by mr W last updated on 14/Jul/21
Commented by mr W last updated on 15/Jul/21
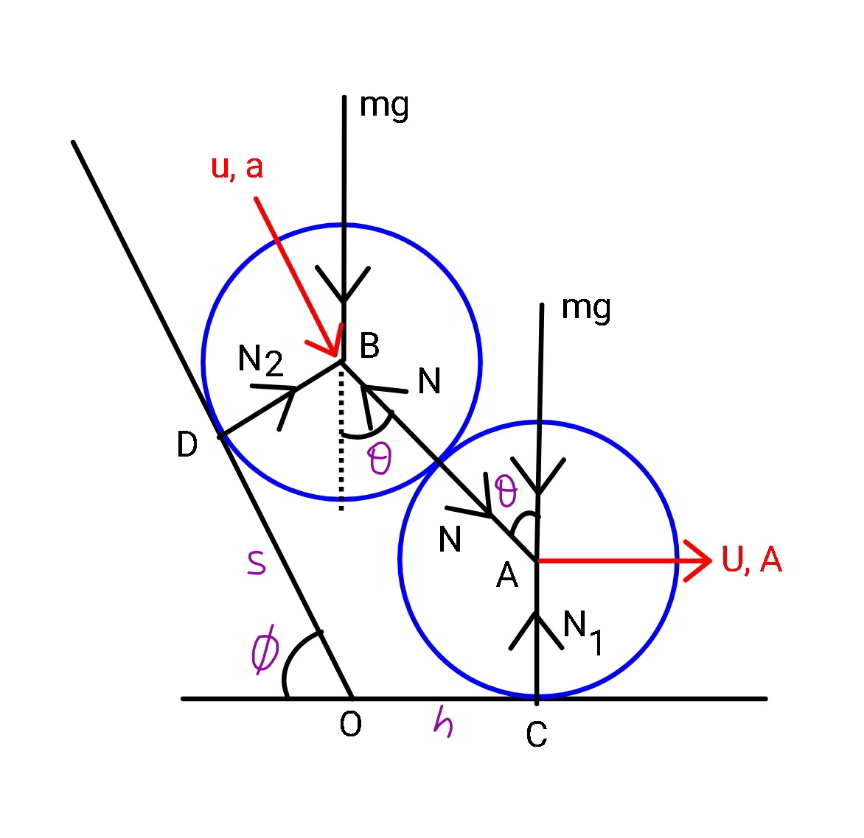
![φ=60° s sin φ+r cos φ=r+2r cos θ ⇒s=((r(1−cos φ))/(sin φ))+((2r cos θ)/(sin φ)) h+s cos φ=r sin φ+2r sin θ ⇒h=r(sin φ−((1−cos φ)/(tan φ)))+2r(sin θ−((cos θ)/(tan φ))) let ω=(dθ/dt) u=(ds/dt)=−((2r sin θ)/(sin φ))ω U=(dh/dt)=2r(cos θ+((sin θ)/(tan φ)))ω y_B =r+2r cos θ Δ(y_(B0) −y_B )=2r(sin φ−cos θ) (m/2)(u^2 +U^2 )=mg2r(sin φ−cos θ) u^2 +U^2 =4gr(sin φ−cos θ) ((4r^2 sin^2 θ)/(sin^2 φ))ω^2 +4r^2 (cos θ+((sin θ)/(tan φ)))^2 ω^2 =4gr(sin φ−cos θ) [((sin^2 θ)/(sin^2 φ))+(cos θ+((sin θ)/(tan φ)))^2 ]ω^2 =(g/r)(sin φ−cos θ) ω=(√(g/r))×(√((sin φ−cos θ)/(((sin^2 θ)/(sin^2 φ))+(cos θ+((sin θ)/(tan φ)))^2 ))) let f(θ)=(√((sin φ−cos θ)/(((sin^2 θ)/(sin^2 φ))+(cos θ+((sin θ)/(tan φ)))^2 ))) f(θ)=sin φ(√((sin φ−cos θ)/(sin^2 θ+sin^2 (θ+φ)))) ω=f(θ)(√(g/r)) A=(dU/dt)=ω(dU/dθ)=2r[ω^2 (−sin θ+((cos θ)/(tan φ)))+ω(cos θ+((sin θ)/(tan φ)))(dω/dθ)] Nsin θ=mA when contact gets lost, N=0 ⇒A=0 ω(−sin θ+((cos θ)/(tan φ)))+(cos θ+((sin θ)/(tan φ)))(dω/dθ)=0 f(θ)(−sin θ+((cos θ)/(tan φ)))+(cos θ+((sin θ)/(tan φ)))((df(θ))/dθ)=0 ⇒tan (θ+φ)((df(θ))/dθ)+f(θ)=0 ⇒θ=... examples: φ=60°, θ_1 ≈35.3946° φ=45°, θ_1 ≈50.3307° ω=(dθ/dt)=(√(g/r)) f(θ) dt=(√(r/g))×(dθ/(f(θ))) t_1 =(√(r/g))×∫_((π/2)−φ) ^θ_1 (dθ/(f(θ))) t_1 =(√(r/g))×(1/(sin φ))∫_((π/2)−φ) ^θ_1 (√((sin^2 θ+sin^2 (θ+φ))/(sin φ−cos θ))) dθ](Q146553.png)
$$\phi=\mathrm{60}° \\ $$$${s}\:\mathrm{sin}\:\phi+{r}\:\mathrm{cos}\:\phi={r}+\mathrm{2}{r}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{s}=\frac{{r}\left(\mathrm{1}−\mathrm{cos}\:\phi\right)}{\mathrm{sin}\:\phi}+\frac{\mathrm{2}{r}\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\phi} \\ $$$${h}+{s}\:\mathrm{cos}\:\phi={r}\:\mathrm{sin}\:\phi+\mathrm{2}{r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{h}={r}\left(\mathrm{sin}\:\phi−\frac{\mathrm{1}−\mathrm{cos}\:\phi}{\mathrm{tan}\:\phi}\right)+\mathrm{2}{r}\left(\mathrm{sin}\:\theta−\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\phi}\right) \\ $$$${let}\:\omega=\frac{{d}\theta}{{dt}} \\ $$$${u}=\frac{{ds}}{{dt}}=−\frac{\mathrm{2}{r}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:\phi}\omega \\ $$$${U}=\frac{{dh}}{{dt}}=\mathrm{2}{r}\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)\omega \\ $$$${y}_{{B}} ={r}+\mathrm{2}{r}\:\mathrm{cos}\:\theta \\ $$$$\Delta\left({y}_{{B}\mathrm{0}} −{y}_{{B}} \right)=\mathrm{2}{r}\left(\mathrm{sin}\:\phi−\mathrm{cos}\:\theta\right) \\ $$$$\frac{{m}}{\mathrm{2}}\left({u}^{\mathrm{2}} +{U}^{\mathrm{2}} \right)={mg}\mathrm{2}{r}\left(\mathrm{sin}\:\phi−\mathrm{cos}\:\theta\right) \\ $$$${u}^{\mathrm{2}} +{U}^{\mathrm{2}} =\mathrm{4}{gr}\left(\mathrm{sin}\:\phi−\mathrm{cos}\:\theta\right) \\ $$$$\frac{\mathrm{4}{r}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{sin}^{\mathrm{2}} \:\phi}\omega^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} \left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} \omega^{\mathrm{2}} =\mathrm{4}{gr}\left(\mathrm{sin}\:\phi−\mathrm{cos}\:\theta\right) \\ $$$$\left[\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{sin}^{\mathrm{2}} \:\phi}+\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} \right]\omega^{\mathrm{2}} =\frac{{g}}{{r}}\left(\mathrm{sin}\:\phi−\mathrm{cos}\:\theta\right) \\ $$$$\omega=\sqrt{\frac{{g}}{{r}}}×\sqrt{\frac{\mathrm{sin}\:\phi−\mathrm{cos}\:\theta}{\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{sin}^{\mathrm{2}} \:\phi}+\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} }} \\ $$$${let}\:{f}\left(\theta\right)=\sqrt{\frac{\mathrm{sin}\:\phi−\mathrm{cos}\:\theta}{\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{sin}^{\mathrm{2}} \:\phi}+\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)^{\mathrm{2}} }} \\ $$$${f}\left(\theta\right)=\mathrm{sin}\:\phi\sqrt{\frac{\mathrm{sin}\:\phi−\mathrm{cos}\:\theta}{\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{2}} \:\left(\theta+\phi\right)}} \\ $$$$\omega={f}\left(\theta\right)\sqrt{\frac{{g}}{{r}}} \\ $$$${A}=\frac{{dU}}{{dt}}=\omega\frac{{dU}}{{d}\theta}=\mathrm{2}{r}\left[\omega^{\mathrm{2}} \left(−\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\phi}\right)+\omega\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)\frac{{d}\omega}{{d}\theta}\right] \\ $$$$ \\ $$$${N}\mathrm{sin}\:\theta={mA} \\ $$$${when}\:{contact}\:{gets}\:{lost}, \\ $$$${N}=\mathrm{0}\:\Rightarrow{A}=\mathrm{0} \\ $$$$\omega\left(−\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\phi}\right)+\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)\frac{{d}\omega}{{d}\theta}=\mathrm{0} \\ $$$${f}\left(\theta\right)\left(−\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\phi}\right)+\left(\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\phi}\right)\frac{{df}\left(\theta\right)}{{d}\theta}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\left(\theta+\phi\right)\frac{{df}\left(\theta\right)}{{d}\theta}+{f}\left(\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\theta=... \\ $$$$ \\ $$$${examples}:\: \\ $$$$\phi=\mathrm{60}°,\:\theta_{\mathrm{1}} \approx\mathrm{35}.\mathrm{3946}° \\ $$$$\phi=\mathrm{45}°,\:\theta_{\mathrm{1}} \approx\mathrm{50}.\mathrm{3307}° \\ $$$$ \\ $$$$\omega=\frac{{d}\theta}{{dt}}=\sqrt{\frac{{g}}{{r}}}\:{f}\left(\theta\right) \\ $$$${dt}=\sqrt{\frac{{r}}{{g}}}×\frac{{d}\theta}{{f}\left(\theta\right)} \\ $$$${t}_{\mathrm{1}} =\sqrt{\frac{{r}}{{g}}}×\int_{\frac{\pi}{\mathrm{2}}−\phi} ^{\theta_{\mathrm{1}} } \frac{{d}\theta}{{f}\left(\theta\right)} \\ $$$${t}_{\mathrm{1}} =\sqrt{\frac{{r}}{{g}}}×\frac{\mathrm{1}}{\mathrm{sin}\:\phi}\int_{\frac{\pi}{\mathrm{2}}−\phi} ^{\theta_{\mathrm{1}} } \sqrt{\frac{\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{2}} \:\left(\theta+\phi\right)}{\mathrm{sin}\:\phi−\mathrm{cos}\:\theta}}\:{d}\theta \\ $$
Commented by ajfour last updated on 15/Jul/21
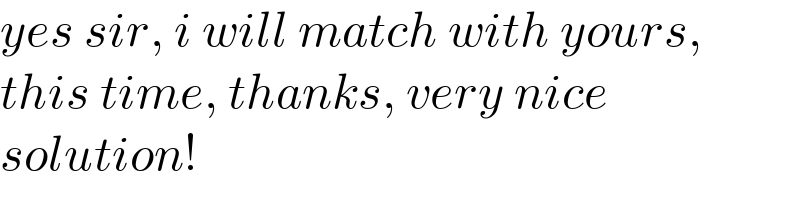
$${yes}\:{sir},\:{i}\:{will}\:{match}\:{with}\:{yours}, \\ $$$${this}\:{time},\:{thanks},\:{very}\:{nice} \\ $$$${solution}! \\ $$
Commented by mr W last updated on 15/Jul/21
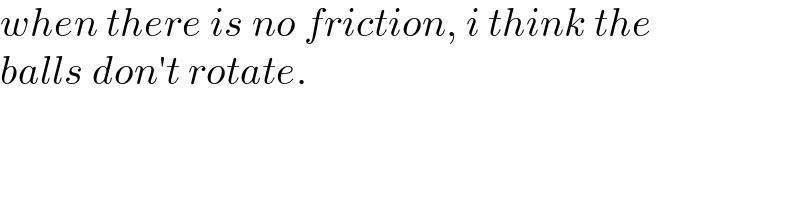
$${when}\:{there}\:{is}\:{no}\:{friction},\:{i}\:{think}\:{the} \\ $$$${balls}\:{don}'{t}\:{rotate}. \\ $$
Commented by otchereabdullai@gmail.com last updated on 16/Jul/21

$$\mathrm{wow}! \\ $$
Answered by ajfour last updated on 14/Jul/21